/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 9223324

Dodaj do ulubionych
Dodaj do rozwiązanych

Romb o kącie ostrym 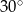∘ 30 jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.

Rozwiązanie

Zaczynamy od rysunku.

PIC

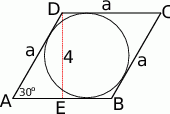
Sposób I

Widać z rysunku, że korzystając z trójkąta prostokątnego 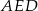AED , możemy wyliczyć długość boku rombu.

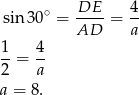
sin 30∘ = DE--= 4- AD a 1 4 --= -- 2 a a = 8.

Teraz łatwo liczymy pole.

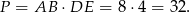
P = AB ⋅ DE = 8 ⋅4 = 32.

Sposób II

Bok rombu mogliśmy też wyliczyć ze wzoru na pole rombu z sinusem

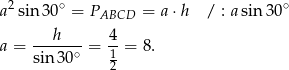
2 ∘ ∘ a sin 30 = PABCD = a ⋅h / : asin3 0 --h---- 4- a = sin 30∘ = 1 = 8. 2

Zatem pole jest równe

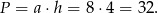
P = a⋅ h = 8⋅ 4 = 32.

 
Odpowiedź: 32

Wersja PDF