/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 9237691

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie prostokątnym krótsza przekątna ma długość ramienia trapezu i dzieli go na dwa trójkąty prostokątne. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

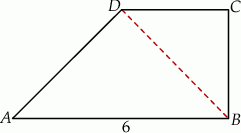
Zauważmy, że trójkąt 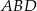ABD jest prostokątny równoramienny, więc 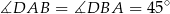∡DAB = ∡DBA = 4 5∘ (jest to połówka kwadratu). Zatem

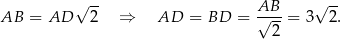
-- -- AB = AD √ 2 ⇒ AD = BD = A√B--= 3√ 2. 2

Trójkąt 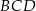BCD jest również połówką kwadratu (bo jest prostokątny i 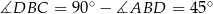∡DBC = 90∘ − ∡ABD = 4 5∘ ), czyli

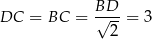
BD-- DC = BC = √ --= 3 2

(mogliśmy też zauważyć, że ramię 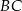BC ma długość wysokości trójkąta 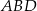ABD , czyli połowie podstawy AB ).

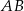Zatem obwód trapezu jest równy

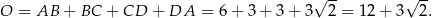
√ -- √ -- O = AB + BC + CD + DA = 6 + 3 + 3 + 3 2 = 12+ 3 2.

 
Odpowiedź: √ -- 12 + 3 2

Wersja PDF