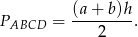/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 9268559

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyprowadź wzór na pole trapezu ze wzorów na pole równoległoboku i trójkąta.

Rozwiązanie

Sposób I

Oznaczmy 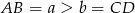AB = a > b = CD . Dorysujmy odcinek 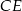CE równoległy do ramienia AD .

PIC

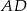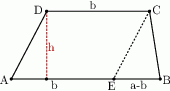
Podzieliliśmy w ten sposób trapez na równoległobok o podstawie 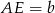AE = b i trójkąt 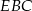EBC , w którym 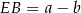EB = a− b . Wysokość każdej z tych figur jest równa 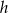h , więc

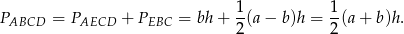
1 1 PABCD = PAECD + PEBC = bh + 2(a− b)h = 2(a+ b)h.

Sposób II

Dorysujmy drugą kopię trapezu odbijając wyjściowy trapez w symetrii względem środka ramienia 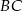BC .

PIC

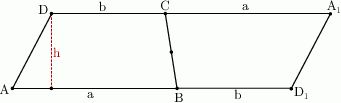
Otrzymamy w ten sposób równoległobok o podstawie 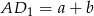AD 1 = a+ b i wysokości 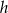h . Pole równoległoboku jest więc równe 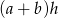(a + b)h . Pole trapezu jest dwa razy mniejsze, czyli

(a-+-b)h- PABCD = 2 .
Wersja PDF