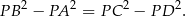Zadanie nr 9292573
Punkt 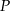 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 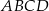 . Wykaż, że
. Wykaż, że 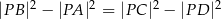 .
.
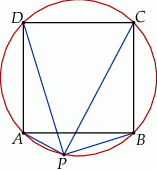
Rozwiązanie
Dorysujmy przekątne kwadratu (a więc średnice okręgu).
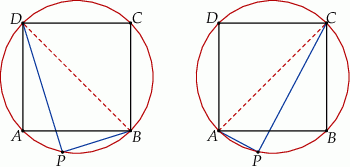
Trójkąty 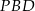 i
i 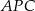 są prostokątne (bo kąt oparty na średnicy jest prosty). Zatem
są prostokątne (bo kąt oparty na średnicy jest prosty). Zatem
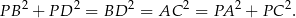
Stąd
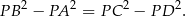
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkt 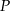 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 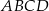 . Wykaż, że
. Wykaż, że 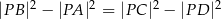 .
.

Dorysujmy przekątne kwadratu (a więc średnice okręgu).

Trójkąty 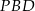 i
i 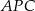 są prostokątne (bo kąt oparty na średnicy jest prosty). Zatem
są prostokątne (bo kąt oparty na średnicy jest prosty). Zatem
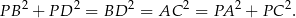
Stąd