/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 9414848

Dodaj do ulubionych
Dodaj do rozwiązanych

Na trapezie 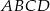ABCD można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe 3√ 3- .

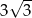Rozwiązanie

Oznaczmy 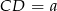CD = a .

PIC

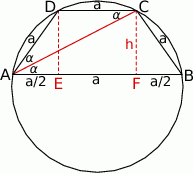
Trapez wpisany w okrąg jest zawsze równoramienny, ponadto

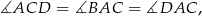
∡ACD = ∡BAC = ∡DAC ,

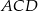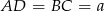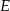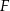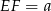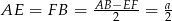więc trójkąt ACD jest równoramienny. Mamy stąd AD = BC = a . Jeżeli ponadto E i F są spodkami wysokości trapezu, to EF = a i AE = FB = AB-−EF-= a 2 2 .

Piszemy teraz twierdzenie Pitagorasa w trójkącie 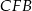CF B .

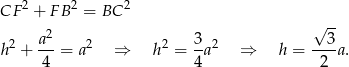
CF 2 + FB 2 = BC 2 √ -- 2 a2- 2 2 3-2 --3- h + 4 = a ⇒ h = 4a ⇒ h = 2 a.

Korzystamy teraz z podanego pola trapezu.

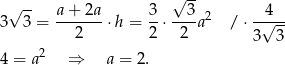
√ -- √ -- a + 2a 3 3 2 4 3 3 = ---2---⋅h = 2-⋅-2-a / ⋅-√--- 3 3 4 = a2 ⇒ a = 2.

Boki trapezu mają więc długości: 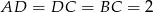AD = DC = BC = 2 , AB = 4 .  
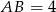Odpowiedź: 2, 2, 2, 4

Wersja PDF