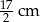Zadanie nr 9515099
Pole rombu jest równe 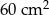 . Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze
. Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze  , że
, że 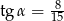 . Oblicz długość boku rombu.
. Oblicz długość boku rombu.
Rozwiązanie
Zaczynamy od rysunku.
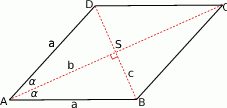
Sposób I
Ponieważ przekątne rombu są prostopadłe oraz dzielą się na połowy, trójkąt 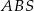 jest prostokątny i ma pole
jest prostokątny i ma pole 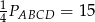 . Korzystając z definicji tangensa w trójkącie
. Korzystając z definicji tangensa w trójkącie 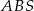 mamy
mamy
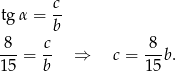
Z drugiej strony, ponieważ pole jest równe 15, mamy
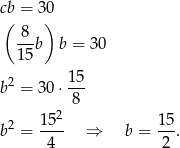
Daje to
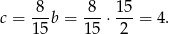
Długość  boku rombu wyliczamy z twierdzenia Pitagorasa.
boku rombu wyliczamy z twierdzenia Pitagorasa.
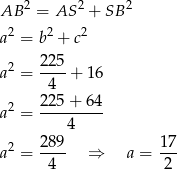
Sposób II
Tym zadanie rozwiążemy używając więcej trygonometrii. Ponieważ pole rombu można liczyć ze wzoru
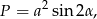
To do wyliczenia boku rombu wystarczy wyliczyć 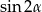 . Można to zrobić na różne sposoby, my wyliczymy najpierw
. Można to zrobić na różne sposoby, my wyliczymy najpierw 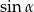 i
i 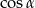 , a potem
, a potem 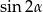 . Liczymy
. Liczymy
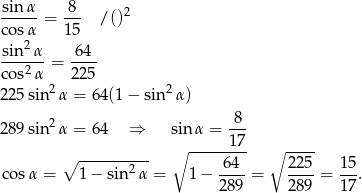
W tym rachunku korzystaliśmy z tego, że  jest kątem ostrym (przy wyborze znaku cosinusa). Mamy więc
jest kątem ostrym (przy wyborze znaku cosinusa). Mamy więc
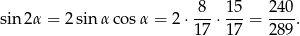
Z podanego pola wyliczamy  .
.
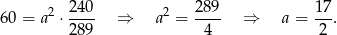
Odpowiedź: