Zadanie nr 9632498
Niech 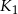 będzie kwadratem o boku długości
będzie kwadratem o boku długości  . Konstruujemy kolejno kwadraty
. Konstruujemy kolejno kwadraty 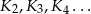 takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów
takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów 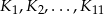 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
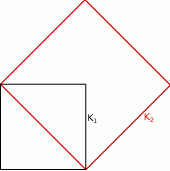
Ze wzoru 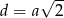 na długość przekątnej kwadratu o boku długości
na długość przekątnej kwadratu o boku długości  , wiemy, że długości boków kwadratów tworzą ciąg geometryczny o pierwszym wyrazie
, wiemy, że długości boków kwadratów tworzą ciąg geometryczny o pierwszym wyrazie  i ilorazie
i ilorazie 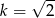 . Ponieważ stosunek pól kwadratów podobnych jest równy kwadratowi skali podobieństwa, pola kwadratów
. Ponieważ stosunek pól kwadratów podobnych jest równy kwadratowi skali podobieństwa, pola kwadratów 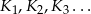 tworzą ciąg geometryczny
tworzą ciąg geometryczny 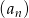 o pierwszym wyrazie
o pierwszym wyrazie 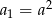 i ilorazie
i ilorazie 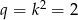 . Suma 11 początkowych wyrazów tego ciągu, to
. Suma 11 początkowych wyrazów tego ciągu, to
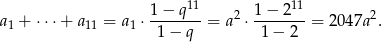
Odpowiedź: