/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 9634518

Dodaj do ulubionych
Dodaj do rozwiązanych

W rombie jedna z przekątnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekątnych pole rombu jest większe od 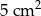5 cm 2 ?

Rozwiązanie

Zacznijmy od szkicowego rysunku.

PIC

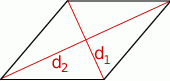
Skorzystamy ze wzoru na pole rombu

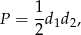
P = 1-d1d2, 2

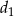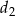gdzie d1 i d2 – długości przekątnych. Oznaczmy 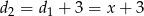d2 = d1 + 3 = x + 3 , zatem

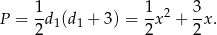
P = 1d 1(d1 + 3 ) = 1x 2 + 3x. 2 2 2

Musimy teraz rozwiązać nierówność

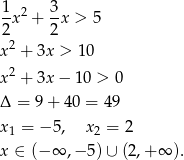
1 3 -x2 + --x > 5 2 2 x 2 + 3x > 10 2 x + 3x − 10 > 0 Δ = 9 + 40 = 49 x 1 = − 5, x2 = 2 x ∈ (−∞ ,− 5) ∪ (2,+ ∞ ).

Zatem krótsza przekątna musi być dłuższa niż 2 cm.  
Odpowiedź: Krótsza przekątna musi być dłuższa niż 2 cm.

Wersja PDF