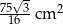Zadanie nr 9783510
W romb, którego bok ma długość 5 cm, a kąt ostry ma miarę 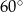 , wpisano okrąg. Oblicz pole czworokąta otrzymanego przez połączenie kolejnych punktów styczności tego okręgu z bokami rombu.
, wpisano okrąg. Oblicz pole czworokąta otrzymanego przez połączenie kolejnych punktów styczności tego okręgu z bokami rombu.
Rozwiązanie
Zadanie to ma wiele możliwych rozwiązań, my pokażemy dwa z nich.
Sposób I
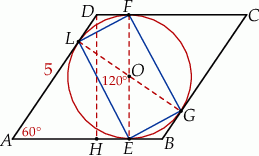
Zaczynamy oczywiście od rysunku.
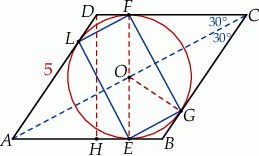
Po pierwsze łatwo jest obliczyć promień  okręgu wpisanego – ponieważ odcinki łączące środek okręgu z punktami styczności są prostopadłe do boków, to średnica
okręgu wpisanego – ponieważ odcinki łączące środek okręgu z punktami styczności są prostopadłe do boków, to średnica 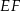 jest dokładnie wysokością rombu. Możemy długość tej średnicy obliczyć z trójkąta prostokątnego
jest dokładnie wysokością rombu. Możemy długość tej średnicy obliczyć z trójkąta prostokątnego 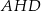 .
.
Interesujący nas czworokąt składa się z dwóch przystających trójkątów prostokątnych  i
i  (są prostokątne bo są oparte na średnicy). Wystarczy obliczyć pole jednego z nich. Przeciwprostokątną tych trójkątów przed chwilą obliczyliśmy, teraz obliczymy ich kąty ostre.
(są prostokątne bo są oparte na średnicy). Wystarczy obliczyć pole jednego z nich. Przeciwprostokątną tych trójkątów przed chwilą obliczyliśmy, teraz obliczymy ich kąty ostre.
Ponieważ odcinki 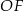 i
i 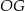 są prostopadłe do odpowiednich boków oraz suma kątów czworokąta
są prostopadłe do odpowiednich boków oraz suma kątów czworokąta 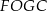 wynosi
wynosi 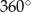 , mamy
, mamy 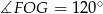 . Trójkąt
. Trójkąt 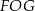 jest równoramienny, więc
jest równoramienny, więc 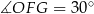 (jeżeli ktoś nie boi się takich rzeczy, to można też było zauważyć, że na czworokącie
(jeżeli ktoś nie boi się takich rzeczy, to można też było zauważyć, że na czworokącie 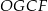 można opisać okrąg, więc
można opisać okrąg, więc 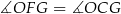 jako kąty wpisane).
jako kąty wpisane).
Obliczyliśmy więc kąt ostry trójkąta 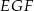 . Znamy też jego przeciwprostokątną, możemy więc obliczyć jego przyprostokątne.
. Znamy też jego przeciwprostokątną, możemy więc obliczyć jego przyprostokątne.
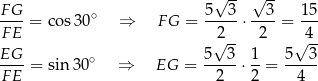
Liczymy pole czworokąta
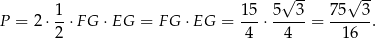
Sposób II
Podobnie jak poprzednio obliczamy wysokość rombu 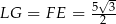 oraz
oraz 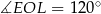 .
.
Tym razem będziemy chcieli skorzystać ze wzoru na pole równoległoboku
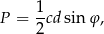
gdzie 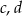 przekątne równoległoboku a
przekątne równoległoboku a 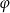 kąt między nimi.
kąt między nimi.
Każdy z kątów 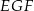 ,
, 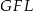 ,
, 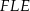 i
i 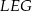 jest oparty na średnicy, zatem czworokąt
jest oparty na średnicy, zatem czworokąt 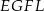 jest prostokątem (można też było zauważyć, że jego przekątne są równej długości i dzielą się na połowy). W szczególności możemy skorzystać z powyższego wzoru na pole.
jest prostokątem (można też było zauważyć, że jego przekątne są równej długości i dzielą się na połowy). W szczególności możemy skorzystać z powyższego wzoru na pole.
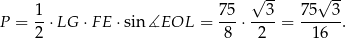
Odpowiedź: