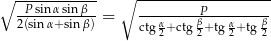Zadanie nr 9875892
Kąty ostre trapezu opisanego na okręgu mają miary  i
i 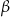 , a pole tego trapezu jest równe
, a pole tego trapezu jest równe 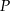 . Oblicz długość promienia okręgu wpisanego w ten trapez.
. Oblicz długość promienia okręgu wpisanego w ten trapez.
Rozwiązanie
Zacznijmy od rysunku.
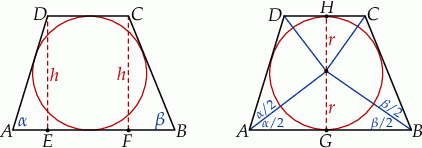
Sposób I
Z trójkątów prostokątnych 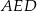 i
i 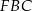 mamy
mamy
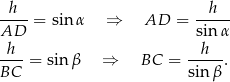
Ponieważ trapez jest opisany na okręgu, więc sumy przeciwległych boków są równe, stąd
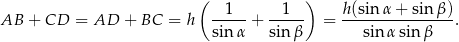
Stąd pole jest równe
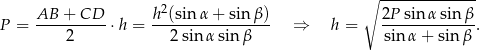
Promień okręgu wpisanego to połowa tej wielkości
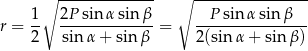
Sposób II
Tym razem dorysujmy dwusieczne kątów trapezu – przetną się one w środku okręgu wpisanego. Ponieważ 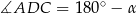 oraz
oraz 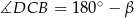 mamy
mamy
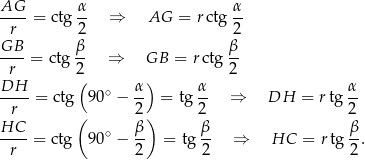
Zatem ze wzoru na pole mamy
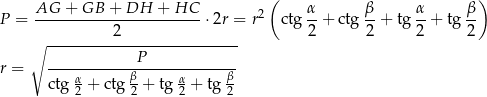
Odpowiedź: