/Szkoła średnia/Zadania maturalne/Matura 2013/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 6 kwietnia 2013 Czas pracy: 180 minut
W kwadracie 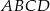 o boku długości 1 na boku
o boku długości 1 na boku 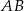 wybrano punkt
wybrano punkt 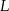 . Na bokach
. Na bokach 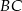 i
i 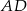 wybrano odpowiednio punkty
wybrano odpowiednio punkty 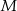 i
i 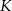 tak, że
tak, że 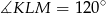 , a dwusieczna tego kąta jest równoległa do boku
, a dwusieczna tego kąta jest równoległa do boku 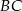 . Oblicz długości odcinków
. Oblicz długości odcinków 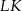 i
i 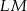 , dla których pole trójkąta
, dla których pole trójkąta 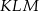 jest największe.
jest największe.
W półkolu z końca średnicy poprowadzono cięciwę, która tworzy ze średnicą kąt o mierze 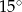 . Oblicz w jakim stosunku zostało podzielone pole tego półkola.
. Oblicz w jakim stosunku zostało podzielone pole tego półkola.
Wyznacz wszystkie wartości parametru 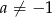 , dla których wykres funkcji
, dla których wykres funkcji 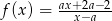 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 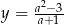 .
.
Kąty 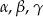 trójkąta
trójkąta 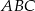 spełniają zależność
spełniają zależność
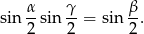
Oblicz wartość wyrażenia 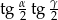 .
.
W czworokącie 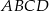 spełniony jest warunek
spełniony jest warunek 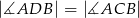 . Wykaż, że na czworokącie
. Wykaż, że na czworokącie 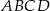 można opisać okrąg.
można opisać okrąg.
Kolejne cyfry dodatniej liczby trzycyfrowej tworzą ciąg geometryczny. Suma cyfr jedności i dziesiątek jest o jeden większa od cyfry setek. Jeżeli od szukanej liczby odejmiemy liczbę złożoną z tych samych cyfr, lecz napisanych w odwrotnej kolejności to otrzymamy 495. Znajdź tę liczbę.
Wyznacz wszystkie liczby 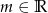 , dla których równanie
, dla których równanie 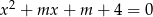 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 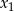 i
i 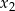 takie, że
takie, że 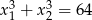 .
.
Udowodnij, że jeżeli 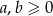 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 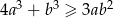 .
.
Obrazem trójkąta 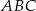 o wierzchołkach
o wierzchołkach 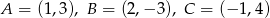 w jednokładności o środku
w jednokładności o środku 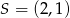 i skali
i skali 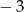 jest trójkąt
jest trójkąt 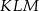 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 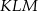 .
.
Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości  oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem
oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Na ile sposobów można rozmieścić sześć ponumerowanych kul w pięciu ponumerowanych szufladach tak, aby w każdej szufladzie była przynajmniej jedna kula.

