/Szkoła średnia/Zadania maturalne/Matura 2013/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 13 kwietnia 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 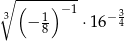 jest równa
jest równa
A) 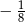 B)
B) 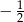 C)
C) 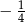 D)
D) 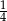
Liczbami spełniającymi równanie 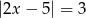 są
są
A) 1 i 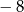 B) 1 i 4 C)
B) 1 i 4 C) 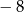 i 4 D)
i 4 D) 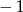 i 4
i 4
Różnica 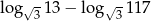 jest równa
jest równa
A) 4 B) 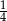 C)
C) 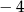 D)
D) 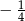
Wartość wyrażenia 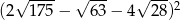 jest równa
jest równa
A) 7 B) 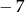 C) 28 D) 14
C) 28 D) 14
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 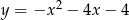 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 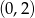 B)
B) 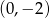 C)
C) 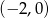 D)
D) 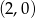
Liczby 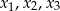 są rozwiązaniami równania
są rozwiązaniami równania 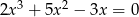 . Suma
. Suma 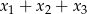 jest równa
jest równa
A) 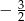 B)
B) 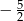 C)
C) 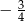 D)
D) 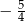
Pierwsza rata, która stanowi 10% ceny aparatu, jest o 19 zł niższa od drugiej raty, która stanowi 15% ceny aparatu. Aparat kosztuje
A) 380 zł B) 38 zł C) 420 zł D) 360 zł
Do wykresu funkcji 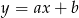 należą punkty
należą punkty 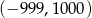 oraz
oraz 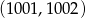 . Wówczas
. Wówczas
A) 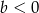 B)
B) 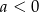 C)
C) 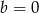 D)
D) 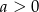
Dane są dwa okręgi o promieniach 12 i 17. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Liczba 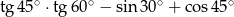 jest równa
jest równa
A) 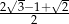 B)
B) 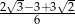 C)
C) 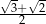 D)
D) 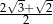
Kąty wewnętrzne przy wierzchołkach 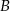 i
i 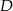 trapezu
trapezu 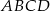 są równe odpowiednio
są równe odpowiednio 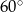 i
i 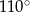 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 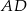 i
i 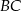 przecinają się pod kątem
przecinają się pod kątem
A) 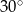 B)
B) 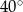 C)
C) 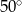 D)
D) 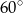
Punkt 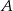 ma współrzędne
ma współrzędne 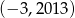 . Punkt
. Punkt 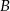 jest symetryczny do punktu
jest symetryczny do punktu 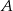 względem osi
względem osi 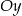 , a punkt
, a punkt 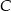 jest symetryczny do punktu
jest symetryczny do punktu 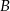 względem osi
względem osi 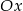 . Punkt
. Punkt 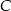 ma współrzędne
ma współrzędne
A) 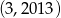 B)
B) 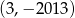 C)
C) 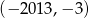 D)
D) 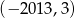
Środek 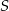 okręgu o równaniu
okręgu o równaniu 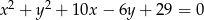 ma współrzędne
ma współrzędne
A) 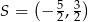 B)
B) 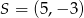 C)
C) 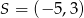 D)
D) 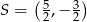
Odcinki 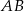 i
i 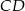 są równoległe (zobacz rysunek). Długość odcinka
są równoległe (zobacz rysunek). Długość odcinka 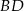 jest równa
jest równa
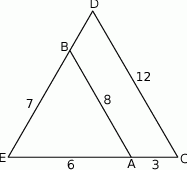
A)  B)
B) 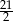 C) 3 D) 2
C) 3 D) 2
Pole prostokąta przedstawionego na rysunku jest równe 18. Zatem
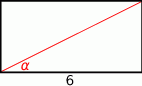
A) 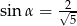 B)
B) 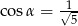 C)
C) 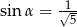 D)
D) 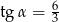
Miara kąta  wynosi
wynosi
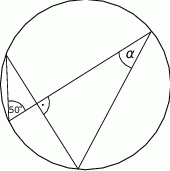
A) 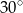 B)
B) 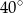 C)
C) 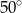 D)
D) 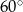
Wiadomo, że wykres funkcji 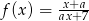 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 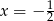 . Wówczas
. Wówczas
A) 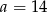 B)
B) 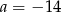 C)
C) 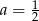 D)
D) 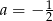
Dany jest ciąg 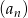 , w którym
, w którym 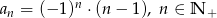 . Jeśli
. Jeśli 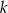 jest liczbą naturalną parzystą, to:
jest liczbą naturalną parzystą, to:
A) 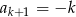 B)
B) 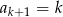 C)
C) 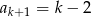 D)
D) 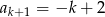
Dwa kolejne wyrazy ciągu geometrycznego 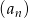 są równe 4 i 24. Wyrazem tego ciągu może być liczba
są równe 4 i 24. Wyrazem tego ciągu może być liczba
A) 96 B) 108 C) 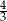 D)
D) 
Ze zbioru liczb 3, 4, 1, 5, 1, 3, 1 usunięto jedną liczbę w ten sposób, że mediana tego zbioru liczb nie uległa zmianie. Usunięta liczba to
A) 1 B) 3 C) 4 D) 5
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 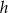 oznacza wysokość, to
oznacza wysokość, to
A) 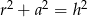 B)
B) 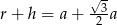 C)
C) 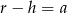 D)
D) 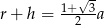
Losujemy jedną liczbę czterocyfrową. Prawdopodobieństwo 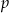 otrzymania liczby, której cyfry to 1,1,2,2 (w dowolnej kolejności) spełnia warunek
otrzymania liczby, której cyfry to 1,1,2,2 (w dowolnej kolejności) spełnia warunek
A) 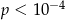 B)
B) 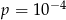 C)
C) 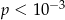 D)
D) 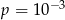
Zadania otwarte
Rozwiąż nierówność 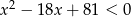 .
.
Rozwiąż równanie 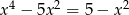 .
.
W trójkącie ostrokątnym 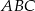 proste
proste 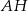 i
i 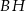 zawierają wysokości poprowadzone z wierzchołków
zawierają wysokości poprowadzone z wierzchołków 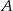 i
i 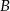 . Uzasadnij, że kąt
. Uzasadnij, że kąt 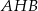 jest rozwarty.
jest rozwarty.
Dane są liczby wymierne 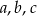 takie, że równanie
takie, że równanie 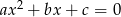 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
Suma 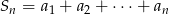 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 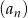 jest określona wzorem
jest określona wzorem 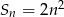 dla
dla 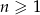 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Kwadrat 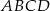 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 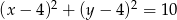 oraz
oraz 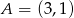 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 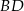 tego kwadratu.
tego kwadratu.
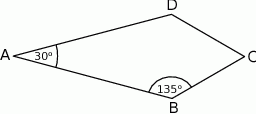
W deltoidzie 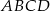 dane są
dane są 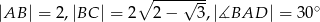 i
i 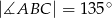 (zobacz rysunek). Oblicz pole tego deltoidu.
(zobacz rysunek). Oblicz pole tego deltoidu.
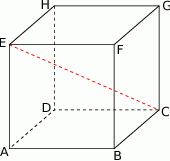
Dany jest sześcian 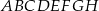 , w którym
, w którym 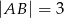 (patrz rysunek). Oblicz odległość wierzchołka
(patrz rysunek). Oblicz odległość wierzchołka 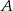 od przekątnej
od przekątnej 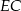 .
.
Dwa samochody odbyły podróż z miejscowości 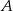 do odległej o 252 km miejscowości
do odległej o 252 km miejscowości 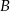 . Średnia prędkość samochodu osobowego na tej trasie była o 24 km/h większa od średniej prędkości samochodu ciężarowego. Oblicz ile czasu zajęła podróż samochodowi osobowemu jeżeli pokonał on tę trasę w czasie o 72 minuty krótszym niż samochód ciężarowy.
. Średnia prędkość samochodu osobowego na tej trasie była o 24 km/h większa od średniej prędkości samochodu ciężarowego. Oblicz ile czasu zajęła podróż samochodowi osobowemu jeżeli pokonał on tę trasę w czasie o 72 minuty krótszym niż samochód ciężarowy.

