Jak sama nazwa wskazuje, układ równań to kilka równań wypisanych pod sobą. Rozwiązanie układu równań polega na znalezieniu liczb, które jednocześnie spełniają wszystkie dane równania.
Rozwiążmy układ równań
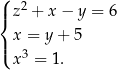
Zauważmy, że z ostatniego równania wynika, że 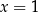 . Podstawiając tę wartość do drugiego równania mamy
. Podstawiając tę wartość do drugiego równania mamy 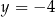 . Na koniec podstawiamy obie wyliczone wartości do pierwszego równania i mamy
. Na koniec podstawiamy obie wyliczone wartości do pierwszego równania i mamy 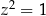 , czyli
, czyli 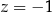 lub
lub 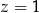 . Układ równań ma więc dwa rozwiązania:
. Układ równań ma więc dwa rozwiązania: 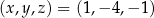 lub
lub 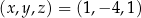 .
.
Jeżeli układ równań nie ma rozwiązań to mówimy, że jest on sprzeczny, a jeżeli ma nieskończenie wiele rozwiązań to mówimy, że układ jest nieoznaczony.
Każde z równań układu
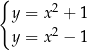
ma oczywiście rozwiązanie, ale nie ma pary liczb 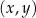 spełniającej oba równania jednocześnie;
spełniającej oba równania jednocześnie; 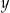 nie może być jednocześnie równe
nie może być jednocześnie równe 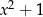 i
i 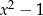 , bo takie założenie prowadzi do równości
, bo takie założenie prowadzi do równości
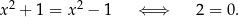
Powyższy układ jest więc sprzeczny.
Rozważmy układ
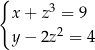
Jeżeli  jest dowolną liczbą rzeczywistą to z równań układu wyliczamy:
jest dowolną liczbą rzeczywistą to z równań układu wyliczamy:
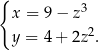
To oznacza, że dla dowolnego 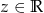 liczby
liczby 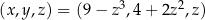 spełniają ten układ równań. Układ ma więc nieskończenie wiele rozwiązań (jest nieoznaczony).
spełniają ten układ równań. Układ ma więc nieskończenie wiele rozwiązań (jest nieoznaczony).
Układy liniowe dwóch równań z dwiema niewiadomymi Najprostszy (nietrywialny) układ równań to układ dwóch równań liniowych z dwiema niewiadomymi.
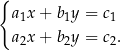
Geometrycznie każde z równań jest równaniem prostej na płaszczyźnie, więc rozwiązania układu równań to punkty wspólne dwóch prostych opisanych przez równania układu. To oznacza, że taki układ równań może być sprzeczny (gdy proste są równoległe i rozłączne), może mieć jedno rozwiązanie (gdy proste nie są równoległe) lub może mieć nieskończenie wiele rozwiązań (gdy proste pokrywają się).
Rozwiązanie układu równań
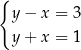
sprowadza się do znalezienia punktów wspólnych prostych 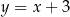 i
i 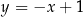 . Bardzo łatwo jest dość dokładnie naszkicować te proste.
. Bardzo łatwo jest dość dokładnie naszkicować te proste.
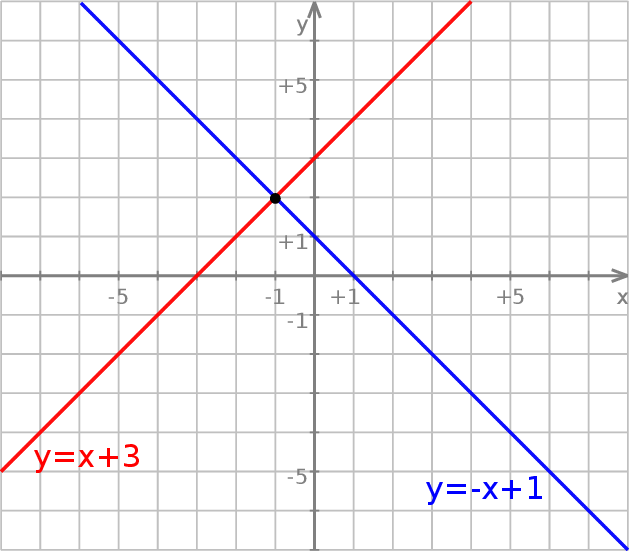
Z obrazka widać, że proste te przecinają się w punkcie 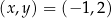 .
.
Jeżeli naszkicujemy proste odpowiadające równaniom układu
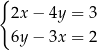
to okaże się, że proste te są równoległe.
To oznacza, że układ równań nie ma rozwiązań.
Jest kilka metod rozwiązywania układów równań liniowych i tym się teraz zajmiemy. Metoda podstawiania W skrócie (dla układu dwóch równań z dwiema niewiadomymi): wyliczamy  lub
lub  z jednego z równań układu i podstawiamy do drugiego równania.
z jednego z równań układu i podstawiamy do drugiego równania.
Rozwiążmy układ równań
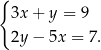
Z pierwszego równania wyliczamy 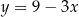 i podstawiamy to wyrażenie do drugiego równania.
i podstawiamy to wyrażenie do drugiego równania.
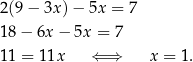
Mamy zatem 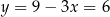 .
.
Tę samą metodę możemy również stosować w przypadku bardziej skomplikowanych układów: z jednego równania układu wyliczamy niewiadomą (w zależności od pozostałych niewiadomych) i wyliczone wyrażenie podstawiamy do pozostałych równań układu. W ten sposób otrzymujemy do rozwiązania prostszy układ równań (który ma jedno równanie i jedną niewiadomą mniej).
Rozwiążmy układ równań
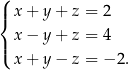
Z pierwszego równania wyliczamy 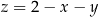 i podstawiamy to wyrażenie do dwóch pozostałych równań.
i podstawiamy to wyrażenie do dwóch pozostałych równań.
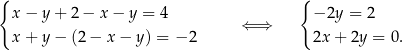
Otrzymujemy stąd 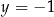 oraz
oraz 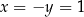 . Liczymy jeszcze
. Liczymy jeszcze  :
: 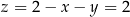 .
.
Metoda przeciwnych współczynników W przypadku liniowego układu dwóch równań z dwiema niewiadomymi: sprowadzamy (mnożąc równania układu przez liczby) układ do postaci, w której współczynniki przy  (lub przy
(lub przy 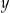 ) różnią się tylko znakiem. Następnie dodajemy równania układu stronami i otrzymujemy równanie z jedną niewiadomą.
) różnią się tylko znakiem. Następnie dodajemy równania układu stronami i otrzymujemy równanie z jedną niewiadomą.
Rozwiążmy układ równań
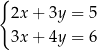
Mnożymy pierwsze równanie układu przez 3, a drugie przez 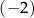 i otrzymujemy
i otrzymujemy
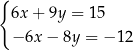
Dodajemy teraz oba równania stronami i dostajemy 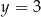 . Zatem
. Zatem
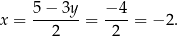
Metoda eliminacji Gaussa Wspomniane wcześniej metody podstawiania i przeciwnych współczynników są tak naprawdę szkolnym wynalazkiem mającym ułatwić uczniom pierwszy kontakt z układami równań. W praktyce układy równań rozwiązuje się odejmując równania układu stronami. Sposób ten (przy odrobinie wprawy) jest szybszy od wspomnianych wcześniej metod.
Rozwiążmy układ równań
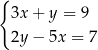
Aby pozbyć się  -ka w drugim równaniu, od drugiego równania odejmujemy pierwsze pomnożone przez 2. Otrzymujemy
-ka w drugim równaniu, od drugiego równania odejmujemy pierwsze pomnożone przez 2. Otrzymujemy
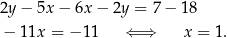
Jeżeli porównacie ten rachunek z tym, który wykonaliśmy (rozwiązując dokładnie ten sam przykład) przy metodzie podstawiania, to nie widać dużej oszczędności. Oszczędność jednak jest, bo przy odrobinie wprawy powyższy rachunek wykonuje się w pamięci, tzn. od razu piszemy, że wynikiem odejmowania równań jest równanie
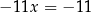
(spróbujcie sprawdzić, że to rzeczywiście można łatwo obliczyć w pamięci!). W przypadku metody podstawiania bardzo trudno jest wykonać taki skrót (trudno jest podstawiać w pamięci).
Podobnie postępujemy w przypadku równań z większą liczbą niewiadomych/równań: odejmując jedno równanie (być może pomnożone przez liczbę) od wszystkich pozostałych równań układu pozbywamy się w tych równaniach jednej niewiadomej. Otrzymujemy w ten sposób prostszy układ, do którego stosujemy tę samą metodę. Konsekwentne stosowanie tego algorytmu (który nosi nazwę metody eliminacji Gaussa) pozwala rozwiązać każdy liniowy układ równań.
Rozwiążmy układ
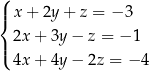
Używamy pierwszego równania do wyeliminowania  -et z dwóch pozostałych równań: do drugiego równania dodajemy pierwsze, a do trzeciego dodajemy pierwsze pomnożone przez 2. Otrzymamy wtedy prostszy układ równań
-et z dwóch pozostałych równań: do drugiego równania dodajemy pierwsze, a do trzeciego dodajemy pierwsze pomnożone przez 2. Otrzymamy wtedy prostszy układ równań
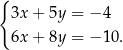
Teraz, aby pozbyć się  -a, dodajemy do drugiego równania pierwsze pomnożone przez
-a, dodajemy do drugiego równania pierwsze pomnożone przez 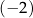 . Mamy zatem
. Mamy zatem
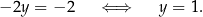
Na koniec obliczamy wartości pozostałych niewiadomych
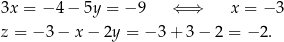
Metoda wyznacznikowa Wyznacznikowa metoda rozwiązywania układów równań została usunięta ze szkolnych programów nauczania, ale czasem bywa użyteczna więc warto wiedzieć o jej istnieniu. W odróżnieniu od wcześniej opisanych metod, nie jest to algorytm rozwiązywania układu równań, ale są to gotowe wzory na rozwiązania.
Wzory są następujące: rozwiązaniem układu równań
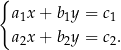
jest para liczb:
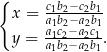
Dobrym ćwiczeniem jest wyprowadzenie tych wzorów – wystarczy rozwiązać powyższy układ równań (z literkami) używając jednej z wcześniej opisanych metod.
Podane wzory mają wady:
-
są skomplikowane, więc trudno je zapamiętać;
-
pojawiają się mianowniki, więc czasem nie działają (gdy w mianowniku jest 0).
Aby uporać się powyższymi problemami wprowadza się specjalną notację.
Liczbę
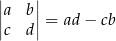
nazywamy wyznacznikiem stopnia 2 z liczb 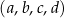 .
.
Powyższą definicję należy rozumieć następująco: z lewej strony równości jest symbol, który definiujemy (i nazywamy wyznacznikiem), a z prawej jest przepis jak wyznacznik obliczać.
Np. 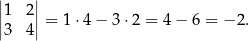
Używając symbolu wyznacznika wzory na rozwiązanie układu równań możemy zapisać trochę estetyczniej:
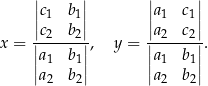
Nadal nie jest idealnie, więc dodatkowo oznaczamy
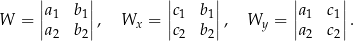
Przy tych oznaczeniach wzory na rozwiązania układu równań pamiętamy w postaci:
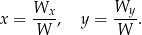
Oczywiście powyższe wzory mają sens tylko dla 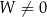 , a dokładniej
, a dokładniej
– Jeżeli 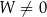 to układ ma dokładnie jedno rozwiązanie
to układ ma dokładnie jedno rozwiązanie 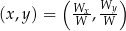 .
.
– Jeżeli 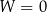 oraz
oraz 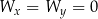 to układ ma nieskończenie wiele rozwiązań.
to układ ma nieskończenie wiele rozwiązań.
– Jeżeli 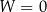 , ale
, ale 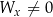 lub
lub 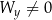 to układ jest sprzeczny.
to układ jest sprzeczny.
Rozwiążmy układ równań
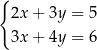
Liczymy wyznaczniki
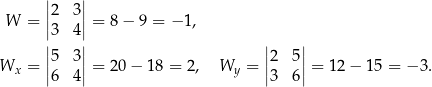
Zatem 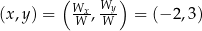 .
.
Rozwiążmy układ równań
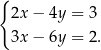
Liczymy wyznaczniki
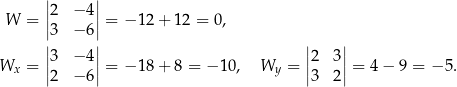
Układ równań jest więc sprzeczny.
Układy równań wielomianowych stopnia 2 Układy stopnia 2 pojawiają się dość naturalnie w zadaniach szkolnych, np. przy szukaniu punktów wspólnych okręgów, w zadaniach z ciągiem geometrycznym, czy też w zadaniach z treścią. Generalna strategia w tego typu równaniach to stosowanie podstawiania tak, aby uzyskać równanie z jedną niewiadomą.
Rozwiążmy układ równań
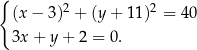
Podstawiamy 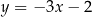 z drugiego równania do pierwszego.
z drugiego równania do pierwszego.
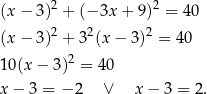
Łatwo stąd wyznaczyć dwa rozwiązania układu: 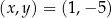 lub
lub 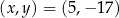 .
.
Rozwiążmy układ równań
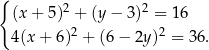
Na pierwszy rzut oka nie widać w jaki sposób podstawić z jednego równania do drugiego, ale sytuacja się uprości, gdy podniesiemy wszystkie wyrażenia do kwadratu.
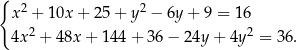
Jeżeli teraz podzielimy drugie równanie przez 4 i odejmiemy pierwsze, to skrócimy kwadraty i otrzymamy
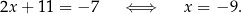
Podstawiamy tę wartość do pierwszego równania wyjściowego układu i mamy
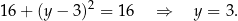
Układy symetryczne Na koniec wspomnimy o bardzo specjalnym typie układów równań, w których równania są wielomianami symetrycznymi, tzn. równania nie ulegają zmianie, gdy zamieniamy niewiadome rolami. Przy rozwiązywaniu tego typu układów wygodnie jest korzystać ze wzorów Viète’a.
Układ równań
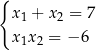
możemy rozwiązać następująco: na mocy wzorów Viète’a rozwiązania tego układu są pierwiastkami równania 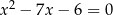 . Daje nam to dwie pary rozwiązań:
. Daje nam to dwie pary rozwiązań: 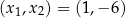 i
i 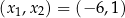 .
.
Opisana metoda może być zastosowana do dowolnego układu równań z dwiema niewiadomymi 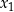 i
i 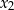 , w którym równania są symetryczne – podstawiamy
, w którym równania są symetryczne – podstawiamy 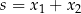 ,
, 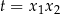 i rozwiązujemy układ (w jakikolwiek sposób), a na koniec wyliczamy
i rozwiązujemy układ (w jakikolwiek sposób), a na koniec wyliczamy 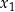 i
i 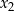 , tak jak to opisaliśmy wyżej.
, tak jak to opisaliśmy wyżej.
W układzie
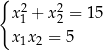
podstawiamy 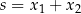 ,
, 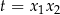 i mamy układ równań
i mamy układ równań
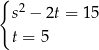
Łatwo z tego układu wyznaczyć 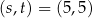 lub
lub 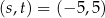 . Zatem
. Zatem 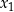 i
i 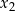 są pierwiastkami równania
są pierwiastkami równania 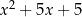 lub
lub 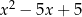 . Daje to nam 4 rozwiązania wyjściowego układu.
. Daje to nam 4 rozwiązania wyjściowego układu.
Tę samą metodę możemy stosować w przypadki większej liczby zmiennych, ale potrzebujemy wtedy wzorów Viète’a dla wielomianów wyższych stopni.
Na mocy wzorów Viète’a liczby spełniające układ równań
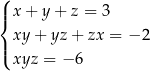
są pierwiastkami równania
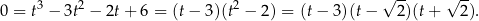
Otrzymujemy stąd 6 rozwiązań układu: 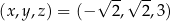 oraz permutacje.
oraz permutacje.

