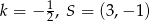Zadanie nr 3410251
Odcinek 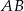 , gdzie
, gdzie 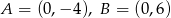 , jest przeciwprostokątną trójkąta prostokątnego
, jest przeciwprostokątną trójkąta prostokątnego 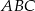 . Wierzchołek
. Wierzchołek 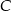 o ujemnej odciętej należy do prostej
o ujemnej odciętej należy do prostej 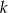 o równaniu
o równaniu 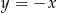 .
.
- Oblicz współrzędne wierzchołka
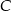 .
. - Obrazem trójkąta
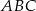 w jednokładności o środku
w jednokładności o środku 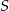 i skali
i skali 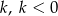 , jest trójkąt
, jest trójkąt 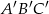 , którego pole wynosi 5. Wiedząc dodatkowo, że
, którego pole wynosi 5. Wiedząc dodatkowo, że 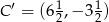 , oblicz skalę jednokładności i współrzędne punktu
, oblicz skalę jednokładności i współrzędne punktu 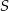 .
.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
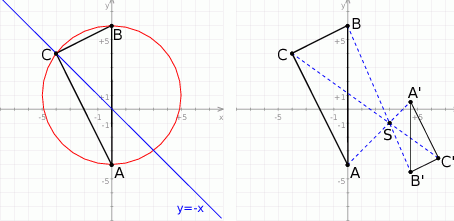
-
Sposób I
Szukamy punktu postaci
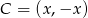 tak, aby suma kwadratów długości przyprostokątnych była równa kwadratowi przeciwprostokątnej.
tak, aby suma kwadratów długości przyprostokątnych była równa kwadratowi przeciwprostokątnej. 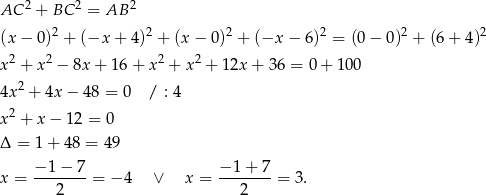
Ponieważ odcięta punktu
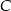 ma być ujemna mamy
ma być ujemna mamy 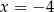 i
i 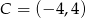 .
. Sposób II
Ponieważ kąt
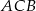 ma być prosty, szukany punkt
ma być prosty, szukany punkt 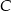 musi być punktem wspólnym danej prostej
musi być punktem wspólnym danej prostej 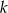 oraz okręgu o środku
oraz okręgu o środku 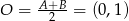 i promieniu
i promieniu 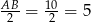 . Okrąg ten ma równanie
. Okrąg ten ma równanie 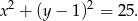
Podstawiamy
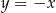 i mamy równanie
i mamy równanie 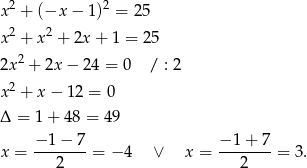
Jak poprzednio stwierdzamy, że
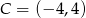 .
. Sposób III
Szukamy punktu
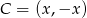 tak, aby
tak, aby 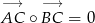 . Daje to nam równanie
. Daje to nam równanie ![0 = [x − 0,−x + 4]∘ [x − 0,−x − 6] = [x,−x + 4]∘ [x,−x − 6] = = x 2 + (x − 4)(x + 6 ) = x2 + x2 + 2x − 24 2 0 = 2x + 2x − 24 / : 2 0 = x 2 + x − 12 .](https://img.zadania.info/zad/3410251/HzadR17x.gif)
Równanie kwadratowe rozwiązujemy jak poprzednio.
Odpowiedź: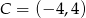
- Ponieważ mamy podane pole trójkąta, który otrzymujemy po jednokładności, policzymy pole trójkąta
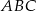 i to pozwoli nam ustalić jaka jest skala
i to pozwoli nam ustalić jaka jest skala 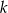 jednokładności.
jednokładności. 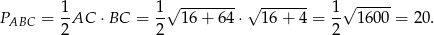
W takim razie
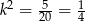 . Ponieważ z założenia
. Ponieważ z założenia 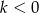 , mamy
, mamy 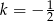 .
. Pozostało wyznaczyć współrzędne punktu
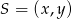 . Punkt ten leży na odcinku
. Punkt ten leży na odcinku 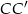 i spełnia równość
i spełnia równość 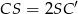 . Używając wektorów możemy to zapisać w postaci
. Używając wektorów możemy to zapisać w postaci ![−→ −→ CS = 2SC ′ [ ] [x + 4 ,y− 4] = 2 13-− x,− 7-− y 2 2 [x + 4 ,y− 4] = [13 − 2x ,− 7− 2y] { x + 4 = 13 − 2x ⇒ x = 3 y − 4 = − 7 − 2y ⇒ y = − 1.](https://img.zadania.info/zad/3410251/HzadR28x.gif)
Zatem
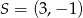
Odpowiedź: