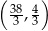Zadanie nr 9920599
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 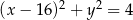 jest okrąg o równaniu
jest okrąg o równaniu 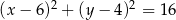 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Rozwiązanie
Możemy zacząć od szkicowego rysunku.
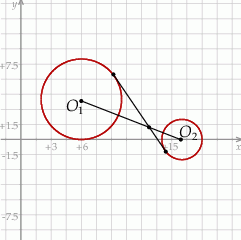
Środek jednokładności dwóch okręgów zawsze leży na prostej przechodzącej przez ich środki 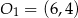 i
i 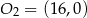 . Takie środki jednokładności są dwa, z informacji o tym, że skala ma być ujemna wynika, że mamy znaleźć ten leżący na odcinku
. Takie środki jednokładności są dwa, z informacji o tym, że skala ma być ujemna wynika, że mamy znaleźć ten leżący na odcinku 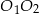 . Jak to zrobić? – to proste, ponieważ promienie podanych okręgów mają długości 2 i 4, więc znamy skalę jednokładności
. Jak to zrobić? – to proste, ponieważ promienie podanych okręgów mają długości 2 i 4, więc znamy skalę jednokładności 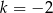 . Musimy więc znaleźć taki punkt
. Musimy więc znaleźć taki punkt 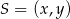 na odcinku
na odcinku 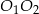 , że
, że 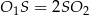 .
.
Sposób I
Najprostszym sposobem wyznaczenia punktu 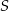 jest użycie wektorów. Mamy równość
jest użycie wektorów. Mamy równość
![O→S = 2S→O 1 2 [x − 6 ,y− 4] = 2[1 6− x,−y ] [x − 6 ,y− 4] = [32 − 2x ,− 2y].](https://img.zadania.info/zad/9920599/HzadR9x.gif)
Porównując współrzędne mamy 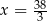 i
i 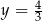
Sposób II
Punkt 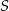 można też wyznaczyć nie używając wektorów, w tym celu wystarczy na prostej
można też wyznaczyć nie używając wektorów, w tym celu wystarczy na prostej 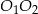 znaleźć punkt, który jest odległy od
znaleźć punkt, który jest odległy od 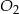 o
o
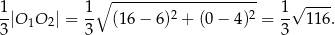
Napiszmy równanie prostej 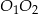 . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty
. Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 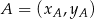 i
i 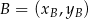 :
:
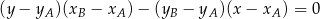
W naszej sytuacji
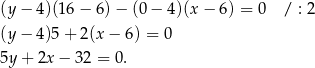
Szukamy na tej prostej punktu 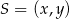 odległego o
odległego o 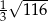 od
od 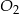
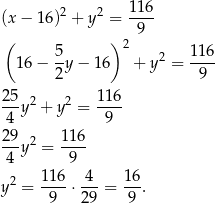
Stąd 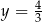 lub
lub 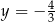 . Drugie z tych rozwiązań odrzucamy, bo punkt
. Drugie z tych rozwiązań odrzucamy, bo punkt 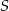 ma być na odcinku
ma być na odcinku 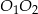 . Z równania prostej mamy wtedy
. Z równania prostej mamy wtedy 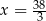 .
.
Odpowiedź: