Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 9192716

Wyznacz równanie okręgu symetrycznego do okręgu 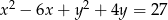2 2 x − 6x + y + 4y = 2 7 względem prostej y = 1 .

Wersja PDF
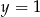Rozwiązanie

Przekształćmy podane równanie okręgu tak, aby było widać jaki ma środek i promień.

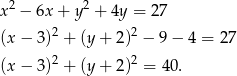
2 2 x − 6x + y + 4y = 2 7 (x− 3)2 + (y+ 2)2 − 9− 4 = 27 (x− 3)2 + (y+ 2)2 = 40.

Jest to więc okrąg o środku w punkcie 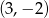(3,− 2) i promieniu √ --- 4 0 .

PIC

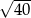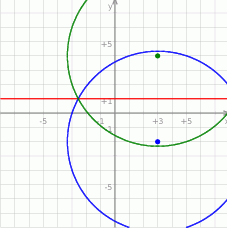
Jeżeli naszkicujemy obrazek, to widać, że szukany okrąg będzie miał ten sam promień i środek 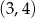(3,4) , czyli będzie to okrąg

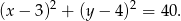
(x − 3)2 + (y − 4)2 = 40.

 
Odpowiedź: (x − 3)2 + (y − 4)2 = 40

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!