/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 1571707

Dodaj do ulubionych
Dodaj do rozwiązanych

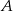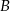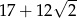Dwa okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy 17 + 12 √ 2- .

PIC

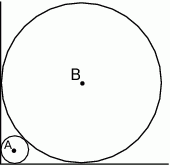
Rozwiązanie

Zaczynamy od dorysowania, wszystkiego co się da.

PIC

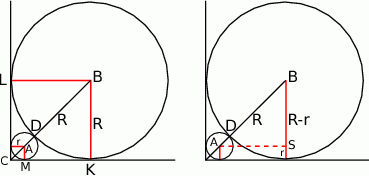
Sposób I

Popatrzmy na trójkąt prostokątny 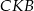CKB . Mamy w nim

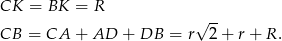
CK = BK = R CB = CA + AD + DB = r√ 2-+ r + R .

Wystarczy teraz napisać twierdzenie Pitagorasa, lub jeszcze prościej, zauważyć, że 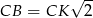√ -- CB = CK 2 (przekątna w kwadracie 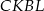CKBL ). Mamy więc

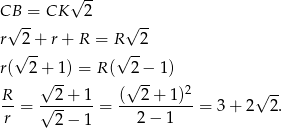
√ -- CB = CK 2 √ -- √ -- r 2+ r+ R = R 2 r(√ 2+ 1) = R (√ 2− 1 ) √ -- √ -- R 2 + 1 ( 2 + 1)2 √ -- r-= √-------= --2-−-1----= 3 + 2 2. 2 − 1

W takim razie stosunek pól okręgów jest równy

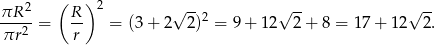
πR 2 ( R ) 2 √ -- √ -- √ -- ----- = -- = (3+ 2 2)2 = 9 + 12 2 + 8 = 17+ 12 2. πr2 r

Sposób II

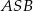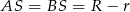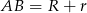Tym razem popatrzmy na trójkąt prostokątny ASB . Jego boki mają długości AS = BS = R − r oraz AB = R + r . Możemy napisać w nim twierdzenie Pitagorasa, albo lepiej zauważyć, że jest to połówka kwadratu, czyli

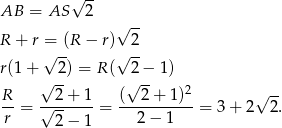
√ -- AB = AS 2 √ -- R + r = (R − r) 2 √ -- √ -- r(1+ 2) = R ( 2− 1 ) √ -- √ -- 2 √ -- R-= √-2-+-1-= (--2-+-1)--= 3 + 2 2. r 2 − 1 2 − 1

Stosunek pól obliczamy tak samo jak w poprzednim sposobie.

Wersja PDF