/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 1764536

Dodaj do ulubionych
Dodaj do rozwiązanych

Z punktu leżącego na okręgu o promieniu 5 poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 2. Oblicz długości tych cięciw.

Rozwiązanie

Niech 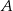A będzie punktem z którego zostały poprowadzone cięciwy 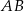AB i AC .

PIC

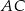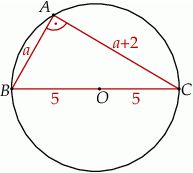
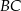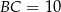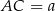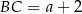Ponieważ cięciwy są prostopadłe, odcinek BC jest średnicą okręgu i BC = 10 . Oznaczmy AC = a i BC = a + 2 . Piszemy teraz twierdzenie Pitagorasa w trójkącie ABC .

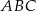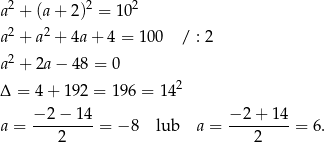
a2 + (a + 2)2 = 102 2 2 a + a + 4a + 4 = 100 / : 2 a2 + 2a − 4 8 = 0 Δ = 4 + 19 2 = 196 = 142 − 2 − 14 − 2 + 14 a = ---------= − 8 lub a = ---------= 6. 2 2

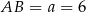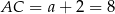Ujemne rozwiązanie odrzucamy i mamy AB = a = 6 . Stąd AC = a + 2 = 8 .  
Odpowiedź: 6 i 8

Wersja PDF