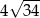/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 2745640

Dodaj do ulubionych
Dodaj do rozwiązanych

W kole o środku 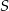S poprowadzono cięciwę, która nie jest średnicą. Punkt 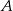A dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek 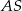AS ma długość 15. Oblicz promień tego koła.

Rozwiązanie

Zaczynamy od rysunku.

PIC

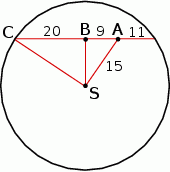
Z podanych informacji wynika, że długość całej cięciwy jest równa 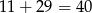11 + 29 = 40 . Zatem 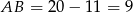AB = 20 − 11 = 9 . Z twierdzenia Pitagorasa w trójkącie 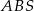ABS mamy

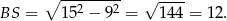
∘ --------- √ ---- BS = 152 − 92 = 144 = 12.

Teraz stosujemy twierdzenie Pitagorasa w trójkącie BCS

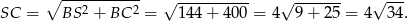
∘ ----------- ---------- ------- √ --- SC = BS2 + BC 2 = √ 1 44+ 400 = 4√ 9 + 25 = 4 34.

 
Odpowiedź: √ --- 4 34

Wersja PDF