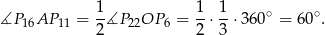Zadanie nr 2816233
Punkty 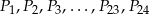 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 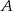 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw 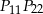 i
i 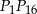 .
.
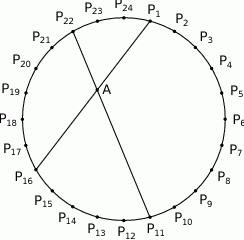
Udowodnij, że 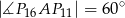 .
.
Rozwiązanie
Sposób I
Połączmy końce cięciw ze środkiem okręgu i dorysujmy cięciwę 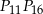 .
.
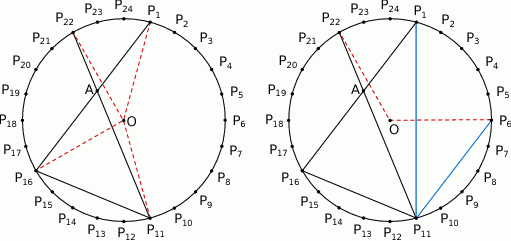
Zauważmy, że kąty środkowe 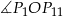 i
i 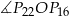 są oparte na łukach, które stanowią odpowiednio
są oparte na łukach, które stanowią odpowiednio 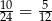 i
i 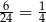 całego okręgu. Mamy zatem
całego okręgu. Mamy zatem
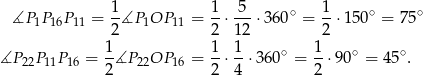
Patrzymy teraz na trójkąt 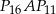 .
.
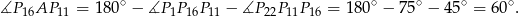
Sposób II
Tym razem dorysujmy cięciwę 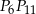 . Zauważmy, że łuki łączące
. Zauważmy, że łuki łączące 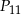 i
i 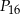 oraz
oraz 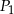 i
i 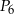 mają tę samą długość, więc
mają tę samą długość, więc
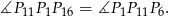
To oznacza, że cięciwy 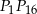 i
i 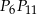 są równoległe. Zatem
są równoległe. Zatem
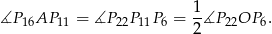
Teraz wystarczy zauważyć, że kąt 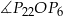 jest oparty na łuku stanowiącym
jest oparty na łuku stanowiącym 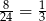 całego okręgu. W takim razie
całego okręgu. W takim razie