Zadanie nr 3257521
W okrąg o środku 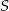 wpisany jest trójkąt równoramienny
wpisany jest trójkąt równoramienny 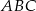 o kącie między ramionami
o kącie między ramionami 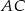 i
i 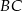 równym
równym 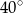 . Przez wierzchołek
. Przez wierzchołek 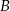 i środek okręgu
i środek okręgu 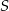 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 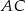 trójkąta w punkcie
trójkąta w punkcie 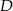 . Wyznacz miarę kąta
. Wyznacz miarę kąta 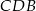 .
.
Rozwiązanie
Zaczynamy od rysunku
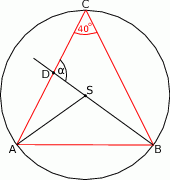
Zauważmy, że
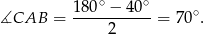
Ponieważ kąt 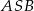 jest kątem środkowym opartym na tym samym łuku co kąt
jest kątem środkowym opartym na tym samym łuku co kąt 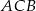 , więc
, więc
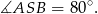
Trójkąt 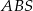 jest równoramienny, więc
jest równoramienny, więc
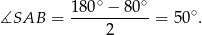
Zatem
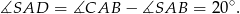
Zauważmy, że
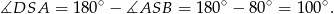
Wyznaczamy kąt 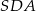
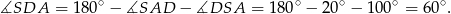
Zatem
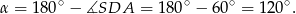
Odpowiedź: