/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 3599668

Dodaj do ulubionych
Dodaj do rozwiązanych

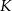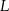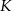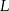Dwa okręgi przecinają się w punktach K i L . Przez punkty K i L poprowadzono proste, które przecinają dane okręgi w punktach 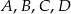A,B ,C,D tak, jak pokazano to na poniższym rysunku. Wykaż, że AC ∥ BD .

PIC

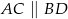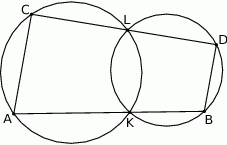
Rozwiązanie

Dorysujmy odcinek 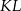KL i oznaczmy ∡A = α .

PIC

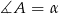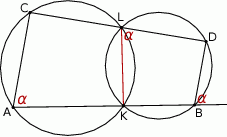
Zauważmy, że czworokąt 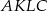AKLC jest wpisany w okrąg, więc

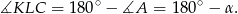
∡KLC = 180 ∘ − ∡A = 180 ∘ − α .

Zatem

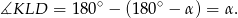
∡KLD = 1 80∘ − (180∘ − α) = α .

Teraz korzystamy z tego, że czworokąt 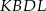KBDL jest wpisany w okrąg.

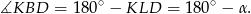
∡KBD = 180∘ − KLD = 180∘ − α .

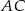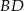To z kolei oznacza, że proste AC i BD przecinają prostą 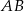AB pod tym samym kątem. Są więc równoległe.

Wersja PDF