Zadanie nr 3641661
Na okręgu o środku 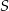 wybrano punkty
wybrano punkty 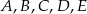 w ten sposób, że odcinek
w ten sposób, że odcinek 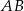 jest średnicą okręgu oraz
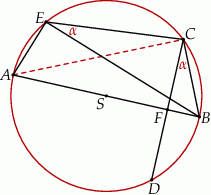
jest średnicą okręgu oraz 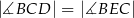 (zobacz rysunek).
(zobacz rysunek).
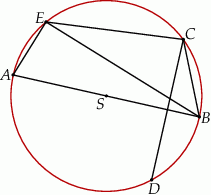
Wykaż, że proste 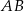 i
i 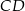 są prostopadłe.
są prostopadłe.
Rozwiązanie
Niech 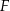 będzie punktem wspólnym prostych
będzie punktem wspólnym prostych 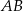 i
i 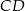 i oznaczmy
i oznaczmy 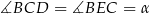 .
.
Sposób I
Wiemy, że 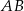 jest średnicą okręgu, więc
jest średnicą okręgu, więc 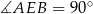 . Ponadto, czworokąt
. Ponadto, czworokąt 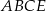 jest wpisany w okrąg, więc
jest wpisany w okrąg, więc
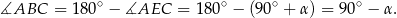
Stąd (patrzymy na trójkąt 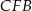 )
)
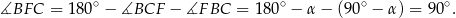
Sposób II
Jeżeli dorysujemy odcinek 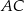 , to trójkąt
, to trójkąt 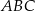 jest prostokątny (bo
jest prostokątny (bo 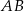 jest średnicą okręgu). Ponadto, trójkąt
jest średnicą okręgu). Ponadto, trójkąt 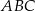 ma dwa takie same kąty jak trójkąt
ma dwa takie same kąty jak trójkąt 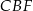 :
:
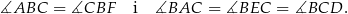
To oznacza, że trójkąt 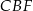 też jest prostokątny i
też jest prostokątny i 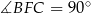 .
.

