/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 4785494

Dodaj do ulubionych
Dodaj do rozwiązanych

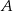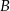Dwa styczne zewnętrznie okręgi o środkach A i B są styczne wewnętrznie do okręgu 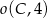o(C ,4) , przy czym punkty 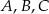A ,B,C nie są współliniowe. Oblicz obwód trójkąta ABC .

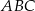Rozwiązanie

Zaczynamy od rysunku.

PIC

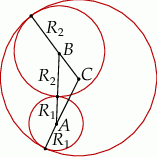
Ponieważ odległość środków okręgów stycznych wewnętrznie jest równa różnicy ich promieni, mamy

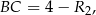
BC = 4− R 2,

gdzie 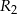R 2 promień okręgu o środku 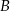B . Podobnie

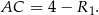
AC = 4− R1.

Mamy zatem

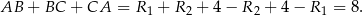
AB + BC + CA = R1 + R 2 + 4 − R 2 + 4− R1 = 8.

 
Odpowiedź: 8

Wersja PDF