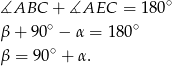/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 5385644

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że jeżeli 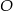O jest środkiem okręgu, na którym leżą punkty 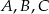A ,B,C , to β = 90 ∘ + α .

PIC

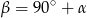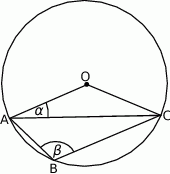
Rozwiązanie

Sposób I

Patrzymy na kąt 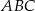ABC i na większy z kątów 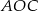AOC jak na kąty oparte na łuku AEC .

PIC

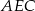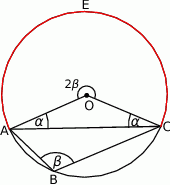
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku mamy więc w trójkącie równoramiennym 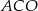ACO

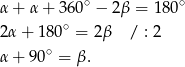
∘ ∘ α + α + 36 0 − 2β = 18 0 2α + 1 80∘ = 2β / : 2 ∘ α + 90 = β.

Sposób II

Przedłużmy promień 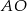AO do jego przecięcia 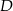D z okręgiem.

PIC

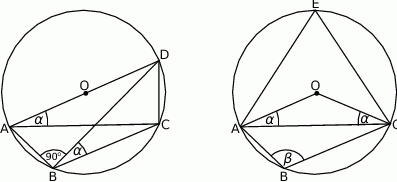
Kąt 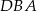DBA jest oparty na średnicy, więc jest to kąt prosty, natomiast 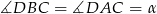∡DBC = ∡DAC = α , bo kąty te są oparte na tym samym łuku. Zatem

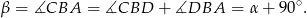
β = ∡CBA = ∡CBD + ∡DBA = α + 90∘.

Sposób III

Tym razem niech punkt 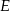E będzie jakimkolwiek punktem okręgu leżącym po przeciwnej stronie cięciwy 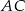AC niż punkt 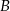B . Trójkąt 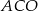ACO jest równoramienny, więc

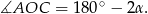
∡AOC = 180∘ − 2α .

Kąt wpisany 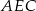AEC jest oparty na tym samym łuku co kąt środkowy 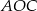AOC , więc

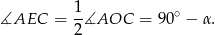
1 ∡AEC = --∡AOC = 90∘ − α. 2

Teraz pozostało skorzystać z faktu, że w czworokącie wpisanym w okrąg sumy przeciwległych kątów są równe 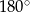∘ 180 . Zatem

∡ABC + ∡AEC = 18 0∘ β + 90 ∘ − α = 180∘ β = 90∘ + α.
Wersja PDF