/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 5388387

Dodaj do ulubionych
Dodaj do rozwiązanych

Odległości środków dwóch okręgów od wierzchołka kąta są równe 8 i 12. Okręgi te są styczne zewnętrznie i każdy z nich jest styczny do obu ramion kąta. Oblicz długości ich promieni.

Rozwiązanie

Zaczynamy naturalnie od rysunku.

PIC

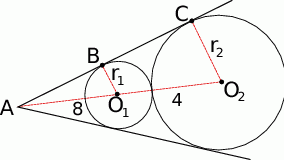
Ponieważ okręgi są styczne zewnętrznie, odległość ich środków jest równa sumie ich promieni

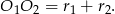
O 1O 2 = r1 + r2.

Z drugiej strony wiemy, że jest równa

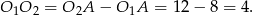
O1O 2 = O 2A − O1A = 12 − 8 = 4.

Zatem

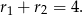
r1 + r2 = 4.

Musimy znaleźć jeszcze jedną zależność między promieniami. Aby to zrobić popatrzmy na prostokątne trójkąty podobne 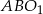ABO 1 i ACO 2 .

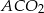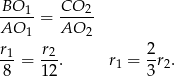
BO 1 CO 2 AO--- = AO--- 1 2 r1 = r2. r = 2-r. 8 12 1 3 2

Podstawiając do wcześniej otrzymanego równania, mamy

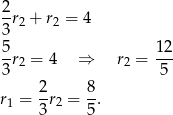
2 --r2 + r2 = 4 3 5-r = 4 ⇒ r = 12- 3 2 2 5 2- 8- r1 = 3 r2 = 5.

 
Odpowiedź: 8 5 i 12- 5

Wersja PDF