Zadanie nr 5482345
Dany jest okrąg o środku w punkcie 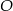 . Prosta
. Prosta 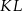 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 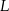 , a środek
, a środek 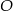 tego okręgu leży na odcinku
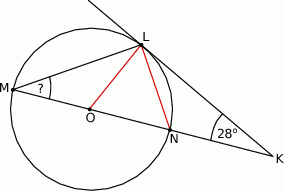
tego okręgu leży na odcinku 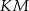 (zob. rysunek). Udowodnij, że kąt
(zob. rysunek). Udowodnij, że kąt 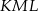 ma miarę
ma miarę 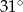 .
.
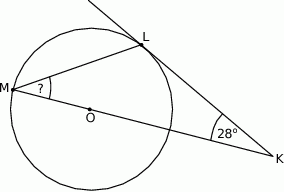
Rozwiązanie
Dorysujmy odcinki 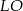 i
i 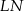 , gdzie
, gdzie 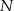 jest drugim końcem średnicy wyznaczonej przez
jest drugim końcem średnicy wyznaczonej przez 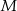 i
i 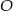 .
.
Trójkąt 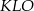 jest prostokątny (bo styczna
jest prostokątny (bo styczna 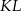 jest prostopadła do promienia
jest prostopadła do promienia 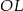 poprowadzonego do punktu styczności). Zatem
poprowadzonego do punktu styczności). Zatem
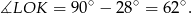
Sposób I
Interesujący nas kąt wpisany 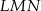 jest oparty na tym samym łuku, co kąt środkowy
jest oparty na tym samym łuku, co kąt środkowy 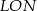 , zatem
, zatem
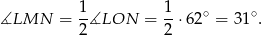
Sposób II
Trójkąt 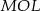 jest równoramienny, więc
jest równoramienny, więc
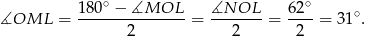
Sposób III
Trójkąt 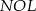 jest równoramienny, a trójkąt
jest równoramienny, a trójkąt 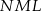 jest prostokątny, więc
jest prostokątny, więc