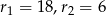/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 5518644

Dodaj do ulubionych
Dodaj do rozwiązanych

Zewnętrznie styczne okręgi o środkach 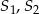S1,S2 i promieniach 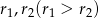r1,r2(r1 > r2) są styczne do prostej 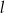l . Kąt między prostą przechodzącą przez środki okręgów i prostą 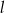l ma miarę 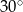30∘ . Wyznacz długości promieni okręgów, jeśli wiadomo, że ich suma jest równa 24.

Rozwiązanie

Zaczynamy od rysunku

PIC

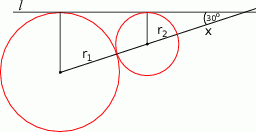
Na podstawie założeń otrzymujemy następujący układ równań

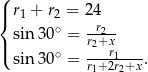
( |{ r1 + r2 = 2 4 sin 30∘ = -r2- |( ∘ r2+xr1 sin 30 = r1+-2r2+x-.

Z drugiego równania wyznaczamy x

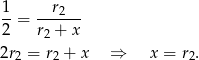
1-= --r2-- 2 r2 + x 2r = r + x ⇒ x = r . 2 2 2

Z pierwszego równania wyznaczamy 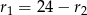r1 = 2 4− r2 . Otrzymane wyniki podstawiamy do trzeciego równania

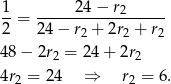
1 24− r --= ------------2----- 2 24 − r2 + 2r2 + r2 48 − 2r2 = 24+ 2r2 4r2 = 2 4 ⇒ r2 = 6.

Zatem

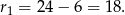
r1 = 2 4− 6 = 18.

 
Odpowiedź: r1 = 18,r2 = 6

Wersja PDF