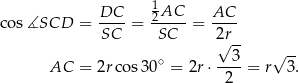Zadanie nr 5912638
Wierzchołki 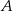 i
i 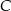 trójkąta
trójkąta 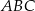 leżą na okręgu o promieniu
leżą na okręgu o promieniu  , a środek
, a środek 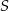 tego okręgu leży na boku
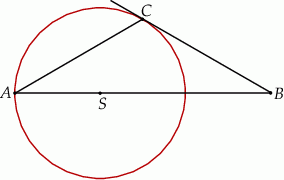
tego okręgu leży na boku 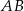 trójkąta (zobacz rysunek). Prosta
trójkąta (zobacz rysunek). Prosta 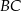 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 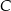 , a ponadto
, a ponadto 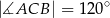 . Wykaż, że
. Wykaż, że 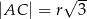 .
.
Rozwiązanie
Dorysujmy promień 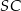 i niech
i niech 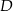 będzie środkiem cięciwy
będzie środkiem cięciwy 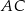 .
.
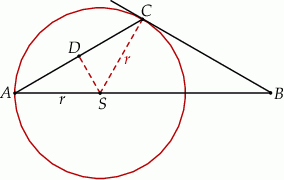
Styczna 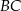 jest prostopadła do promienia
jest prostopadła do promienia 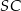 , więc
, więc
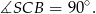
Stąd
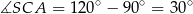
oraz