Zadanie nr 6385719
Na okręgu o promieniu  wybrano punkty
wybrano punkty 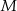 i
i 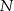 w ten sposób, że proste
w ten sposób, że proste 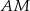 i
i 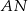 są styczne do okręgu. Punkt
są styczne do okręgu. Punkt 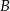 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 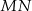 i prostej łączącej
i prostej łączącej 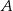 ze środkiem
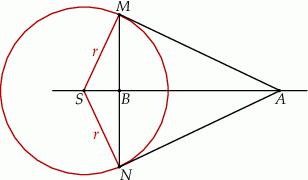
ze środkiem 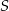 tego okręgu. Wykaż, że
tego okręgu. Wykaż, że 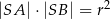 .
.
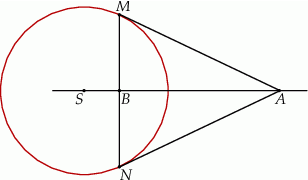
Rozwiązanie
Połączmy środek okręgu 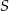 z punktem
z punktem 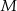 .
.
Styczna jest prostopadła do promienia okręgu, więc trójkąt 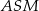 jest prostokątny. Ponadto prosta
jest prostokątny. Ponadto prosta 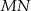 jest prostopadła do
jest prostopadła do 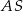 (bo np.
(bo np. 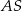 jest to dwusieczną w trójkącie równoramiennym
jest to dwusieczną w trójkącie równoramiennym 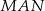 ), więc odcinek
), więc odcinek 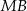 jest wysokością trójkąta
jest wysokością trójkąta 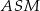 .
.
Zauważmy teraz, że trójkąty 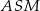 i
i 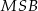 są podobne (oba są prostokątne i mają wspólny kąt ostry
są podobne (oba są prostokątne i mają wspólny kąt ostry 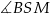 ). W takim razie
). W takim razie