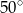/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 6982953

Dodaj do ulubionych
Dodaj do rozwiązanych

Wiedząc, że punkt 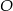O jest środkiem okręgu, oblicz miarę kąta α .

PIC

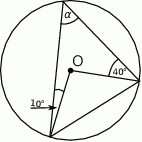
Rozwiązanie

Sposób I

Dorysujmy odcinek 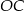OC .

PIC

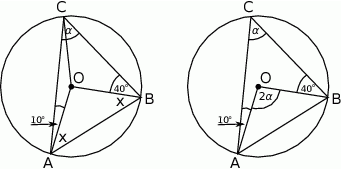
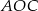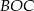Zauważmy, że trójkąty AOC i BOC są równoramienne, więc

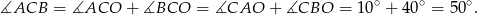
∘ ∘ ∘ ∡ACB = ∡ACO + ∡BCO = ∡CAO + ∡CBO = 10 + 40 = 50 .

Sposób II

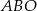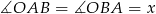Zauważmy, że trójkąt ABO jest równoramienny, oznaczmy ∡OAB = ∡OBA = x .

Mamy wtedy

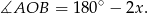
∡AOB = 180∘ − 2x .

Ponadto kąt 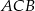ACB jest oparty na tym samym łuku co kąt 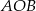AOB , więc

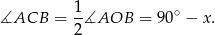
∡ACB = 1-∡AOB = 90∘ − x. 2

Obliczmy teraz sumę kątów w trójkącie 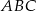ABC .

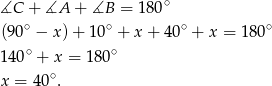
∘ ∡C + ∡A + ∡B = 180 (90 ∘ − x )+ 1 0∘ + x+ 40∘ + x = 180 ∘ ∘ ∘ 14 0 + x = 180 x = 40∘.

Stąd 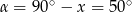α = 90 ∘ − x = 50∘ .

Sposób III

Kąt wypukły 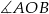∡AOB ma miarę 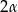2α (bo jest kątem środkowym opartym na tym samym łuku co kąt wpisany 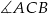∡ACB ). Zatem kąt wklęsły 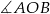∡AOB ma miarę 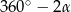36 0∘ − 2α . Suma kątów czworokąta wklęsłego 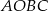AOBC jest równa 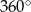360∘ , co prowadzi do równania.

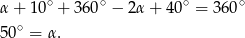
α + 10 ∘ + 36 0∘ − 2α+ 40∘ = 36 0∘ ∘ 50 = α.

 
Odpowiedź: 50∘

Wersja PDF