/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 7011351

Dodaj do ulubionych
Dodaj do rozwiązanych

W okręgu o promieniu 8 cm poprowadzono cięciwę 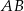AB . Długość łuku 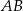AB jest równa 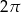2π . Oblicz miarę kąta ostrego zawartego między cięciwą 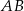AB a styczną do okręgu w punkcie A .

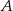Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

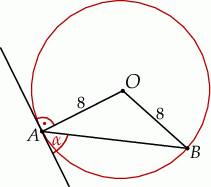
Z podanej długości łuku obliczmy najpierw miarę kąta środkowego 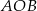AOB .

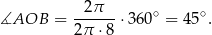
∡AOB = -2π---⋅360∘ = 45∘. 2π ⋅8

Ponieważ trójkąt 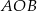AOB jest równoramienny, więc

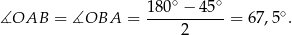
∘ ∘ ∡OAB = ∡OBA = 180--−-45-- = 67,5∘. 2

Ponieważ styczna jest prostopadła do promienia 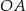OA mamy

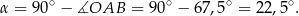
∘ ∘ ∘ ∘ α = 90 − ∡OAB = 90 − 67,5 = 22,5 .

 
Odpowiedź: 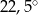22,5 ∘ .

Wersja PDF