/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 7036046

Dodaj do ulubionych
Dodaj do rozwiązanych

Z półokręgów budujemy krzywą (patrz rysunek). Pierwszy półokrąg ma promień długości 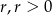r,r > 0 , a promień każdego następnego półokręgu stanowi 23 promienia poprzedniego. Niech n oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej n długość krzywej jest mniejsza od 3πr .

PIC

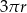Rozwiązanie

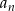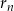Jeżeli oznaczymy przez an długość n -tego półokręgu, a przez rn jego promień to

a1 = πr

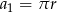
oraz

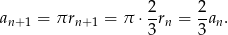
an+ 1 = πrn +1 = π ⋅ 2rn = 2-an. 3 3

Zatem mamy do czynienia z ciągiem geometrycznym 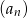(an) o pierwszym wyrazie 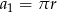a1 = πr i ilorazie q = 23 .

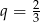Sposób I

Ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy

[ ( ) ] 1 − qn 1− (23)n 2 n Sn = a1 ⋅-1−--q-= πr -----2---= 3 πr 1− 3- 1 − 3

Teraz wystarczy zauważyć, że

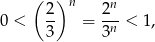
( )n n 0 < 2- = 2--< 1, 3 3n

czyli

[ ( 2)n ] Sn = 3πr 1 − -- < 3πr. 3

Sposób II

Ze wzoru na sumę wyrazów szeregu geometrycznego wiemy, że suma wszystkich wyrazów ciągu 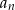an jest równa

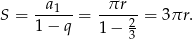
a1 πr S = ------= ----2-= 3πr . 1 − q 1 − 3

W takim razie każda z sum częściowych musi być mniejsza od 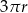3πr .

Wersja PDF