Zadanie nr 7065210
Na okręgu o środku 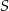 wybrano punkty
wybrano punkty 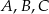 i
i 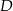 w ten sposób, że prosta
w ten sposób, że prosta 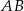 zawiera punkt
zawiera punkt 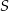 , a proste
, a proste 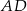 i
i 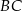 przecinają się w punkcie
przecinają się w punkcie 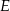 . Punkt
. Punkt 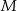 jest punktem wspólnym prostych
jest punktem wspólnym prostych 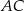 i
i 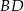 . Wykaż, że proste
. Wykaż, że proste 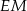 i
i 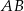 są prostopadłe.
są prostopadłe.
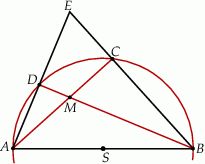
Rozwiązanie
Zauważmy, że każdy z kątów 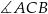 i
i 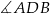 jest oparty na średnicy, więc oba te kąty są proste.
jest oparty na średnicy, więc oba te kąty są proste.
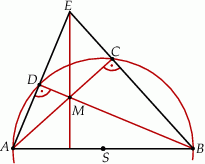
To oznacza, że proste 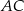 i
i 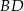 są wysokościami trójkąta
są wysokościami trójkąta 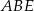 . Jednak wszystkie trzy wysokości w trójkącie przecinają się w jednym punkcie, więc prosta
. Jednak wszystkie trzy wysokości w trójkącie przecinają się w jednym punkcie, więc prosta 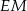 jest trzecią wysokością trójkąta
jest trzecią wysokością trójkąta 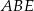 . Jest więc ona prostopadła do prostej
. Jest więc ona prostopadła do prostej 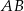 .
.

