/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 7257779

Dodaj do ulubionych
Dodaj do rozwiązanych

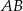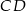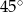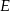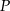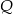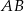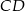W okręgu o promieniu 6 średnice AB i CD przecinają się pod kątem ∘ 45 . Na okręgu tym wybrano punkt E oraz skonstruowano jego rzuty P i Q odpowiednio na średnice AB i CD . Oblicz długość odcinka PQ .

PIC

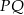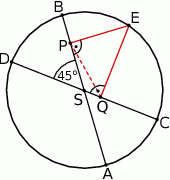
Rozwiązanie

Dorysujmy odcinek 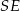SE .

PIC

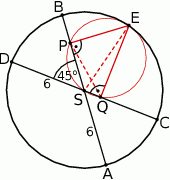
Zauważmy, że w czworokącie 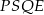P SQE dwa przeciwległe kąty są proste, więc na czworokącie tym można opisać okrąg, którego średnicą jest 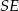SE . Aby obliczyć długość odcinka 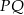PQ wystarczy zastosować twierdzenie sinusów do trójkąta P SQ .

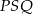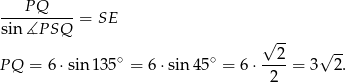
PQ ----------= SE sin ∡P SQ √ -- ∘ ∘ --2- √ -- P Q = 6⋅ sin 135 = 6⋅sin 45 = 6 ⋅ 2 = 3 2.

 
Odpowiedź: P Q = 3√ 2-

Wersja PDF