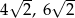Zadanie nr 8091316
Dwie cięciwy przecinają się wewnątrz okręgu tak, że odcinki jednej z nich mają długości 8 i 6, a odcinki drugiej pozostają w stosunku 2:3. Podaj długości odcinków drugiej cięciwy.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
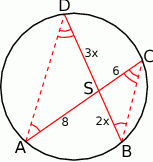
Sposób I
Jeżeli połączymy końce narysowanych cięciw oraz zaznaczymy kąty wpisane oparte na tych samych łukach, to widać, że otrzymamy dwa trójkąty podobne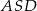 
oraz 
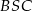. Z podobieństwa tych trójkątów otrzymujemy
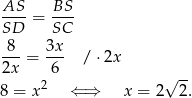
Zatem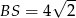 
i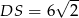 
.
Sposób II
Mogliśmy też od razu skorzystać z twierdzenia o odcinkach siecznych
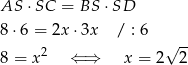
Zatem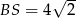 
i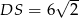 
.
Odpowiedź: 
