Zadanie nr 9276365
Średnica 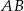 i cięciwa
i cięciwa 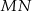 okręgu przecinają się w punkcie
okręgu przecinają się w punkcie 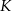 . Kąt
. Kąt 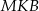 ma miarę
ma miarę 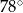 , a kąt środkowy oparty na łuku
, a kąt środkowy oparty na łuku 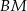 ma miarę
ma miarę 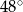 . Wyznacz miarę kąta
. Wyznacz miarę kąta 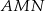 .
.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
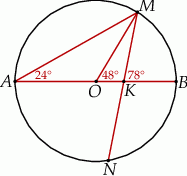
Niektóre rzeczy powinny się narzucać: ponieważ kąt wpisany jest zawsze połową kąta środkowego opartego na tym samym łuku, mamy
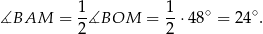
Popatrzmy na trójkąt 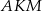 . Mamy wyliczyć jeden z jego kątów (ten przy wierzchołku
. Mamy wyliczyć jeden z jego kątów (ten przy wierzchołku 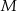 ), więc wystarczy wyliczyć jego pozostałe dwa kąty. Miarę kąt przy wierzchołku
), więc wystarczy wyliczyć jego pozostałe dwa kąty. Miarę kąt przy wierzchołku 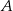 już znamy, więc pozostaje kąt przy wierzchołku
już znamy, więc pozostaje kąt przy wierzchołku 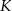 :
:
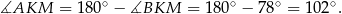
Zatem
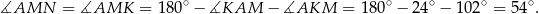
Odpowiedź: