Zadanie nr 9508382
Trójkąt 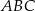 jest trójkątem równobocznym o boku długości
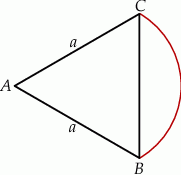
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami
. Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami 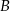 i
i 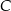 ma długość większą niż
ma długość większą niż 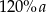 .
.
Rozwiązanie
Dorysujmy cały okrąg opisany na trójkącie 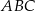 .
.
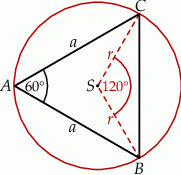
Promień okręgu opisanego na trójkącie równobocznym o boku  jest równy
jest równy
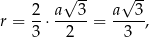
a interesujący nas łuk, to 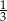 tego okręgu. Zatem długość tego łuku jest równa
tego okręgu. Zatem długość tego łuku jest równa
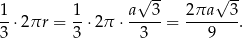
Pozostało wykazać, że liczba ta jest większa od
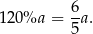
Przekształcamy nierówność, którą mamy udowodnić w sposób równoważny.
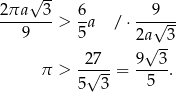
Łatwo teraz sprawdzić na kalkulatorze, że 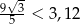 , a jednocześnie
, a jednocześnie 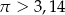 . To oznacza, że otrzymana nierówność jest spełniona. Ponieważ przekształcaliśmy nierówność przy pomocy równoważności, wyjściowa nierówność też jest prawdziwa.
. To oznacza, że otrzymana nierówność jest spełniona. Ponieważ przekształcaliśmy nierówność przy pomocy równoważności, wyjściowa nierówność też jest prawdziwa.

