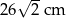Zadanie nr 9663131
Do dwóch okręgów o promieniach długości 3 cm i 10 cm poprowadzono wspólną styczną tak, że okręgi znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm. Oblicz długość odcinka między punktami styczności.
Rozwiązanie
Zaczynamy naturalnie od schematycznego rysunku.
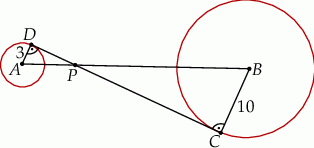
Trójkąty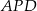 
i 
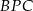są prostokątne i mają wspólny kąt przy wierzchołku 
– są zatem podobne. Mamy zatem
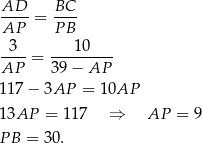
Stąd
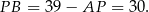
Pozostało obliczyć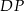 
i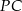 
. Korzystamy z twierdzenia Pitagorasa
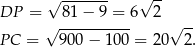
Zatem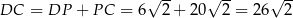 
.
Odpowiedź: 
