/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Zadanie nr 9693186

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są trzy okręgi o środkach 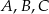A ,B ,C i promieniach równych odpowiednio 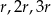r,2r,3r . Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie 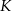K , drugi z trzecim w punkcie 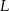L i trzeci z pierwszym w punkcie 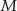M . Oblicz stosunek pola trójkąta 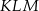KLM do pola trójkąta ABC .

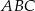Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

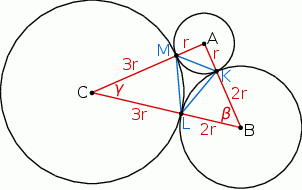
Zauważmy najpierw, że boki trójkąta 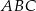ABC mają długości 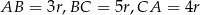AB = 3r,BC = 5r,CA = 4r . Jest to więc trójkąt prostokątny. W szczególności

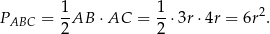
P = 1AB ⋅AC = 1-⋅3r⋅ 4r = 6r2. ABC 2 2

Specjalnie nie widać jak obliczyć pole trójkąta 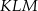KLM , ale za to łatwo jest obliczyć pola trójkątów 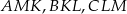AMK ,BKL ,CLM . Korzystamy ze wzoru z sinusem.

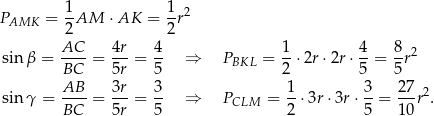
1- 1-2 PAMK = 2AM ⋅AK = 2r AC 4r 4 1 4 8 sin β = ---- = --= -- ⇒ PBKL = --⋅2r⋅ 2r⋅ --= --r2 BC 5r 5 2 5 5 sin γ = AB--= 3r-= 3- ⇒ P = 1⋅ 3r⋅3r ⋅ 3-= 27r2. BC 5r 5 CLM 2 5 10

W takim razie

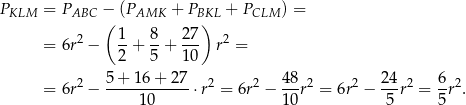
PKLM = PABC − (PAMK + PBKL + PCLM ) = ( ) = 6r2 − 1-+ 8+ 27- r2 = 2 5 10 5 + 1 6+ 2 7 48 2 4 6 = 6r2 − ------------⋅ r2 = 6r2 − --r2 = 6r2 − ---r2 = --r2. 10 10 5 5

Interesujący nas iloraz jest więc równy

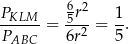
PKLM 65 r2 1 ------= --2-= -. PABC 6r 5

 
Odpowiedź: 1 5

Wersja PDF