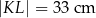Zadanie nr 9746893
W danym okręgu o środku  poprowadzono cięciwy
poprowadzono cięciwy  i
i  , które przecięły się w punkcie
, które przecięły się w punkcie 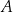 .
.

-
Wykaż, że trójkąty
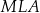 i
i 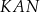 są podobne.
są podobne. -
Wiedząc, że
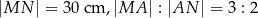 oraz
oraz 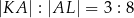 , oblicz długość cięciwy
, oblicz długość cięciwy 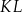 .
.
Rozwiązanie
Dorysujmy odcinki 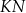 i
i 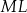 .
.

-
Ponieważ kąty
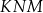 i
i 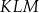 są kątami wpisanymi opartymi na tym samym łuku, więc
są kątami wpisanymi opartymi na tym samym łuku, więc 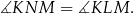
Podobnie, kąty
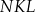 i
i 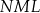 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc 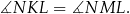
Zatem
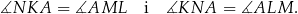
Ponieważ trójkąty mają dwa takie same kąty, więc muszą być podobne.
-
Ponieważ
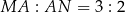 , możemy oznaczyć
, możemy oznaczyć 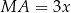 i
i 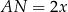 dla pewnego
dla pewnego  . Wiemy ponadto, że
. Wiemy ponadto, że 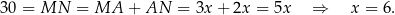
Zatem
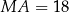 i
i 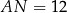 .
. Korzystając z drugiej z podanych proporcji
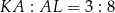 , możemy oznaczyć
, możemy oznaczyć 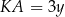 i
i 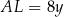 . Korzystamy teraz z podobieństwa trójkątów
. Korzystamy teraz z podobieństwa trójkątów 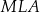 i
i 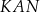 .
. 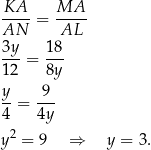
Zatem
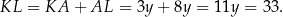
Odpowiedź: