/Szkoła średnia/Zadania maturalne/Matura 2013/Matura
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 27 sierpnia 2013 Czas pracy: 170 minut
Zadania zamknięte
Wskaż rysunek, na którym przedstawiony jest zbiór rozwiązań nierówności 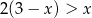 .
.

Gdy od 17% liczby 21 odejmiemy 21% liczby 17, to otrzymamy
A) 0 B) 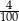 C) 3,57 D) 4
C) 3,57 D) 4
Liczba 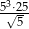 jest równa
jest równa
A) 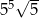 B)
B) 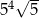 C)
C) 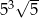 D)
D) 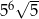
Rozwiązaniem układu równań 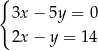 jest para
jest para 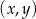 liczb takich, że
liczb takich, że
A) 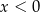 i
i 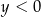 B)
B) 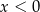 i
i 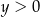 C)
C) 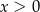 i
i 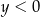 D)
D) 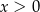 i
i 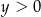
Funkcja 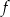 jest określona wzorem
jest określona wzorem 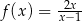 dla
dla 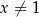 . Wartość funkcji
. Wartość funkcji 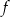 dla argumentu
dla argumentu 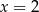 jest równa
jest równa
A) 2 B) 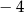 C) 4 D)
C) 4 D) 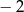
Liczby rzeczywiste 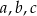 spełniają warunki:
spełniają warunki: 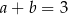 ,
, 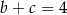 i
i 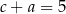 . Wtedy suma
. Wtedy suma 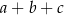 jest równa
jest równa
A) 20 B) 6 C) 4 D) 1
Prostą równoległą do prostej o równaniu 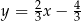 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 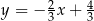 B)
B) 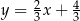 C)
C) 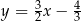 D)
D) 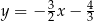
Dla każdych liczb rzeczywistych 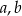 wyrażenie
wyrażenie 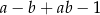 jest równe
jest równe
A) 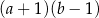 B)
B) 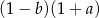 C)
C) 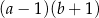 D)
D) 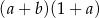
Wierzchołek paraboli o równaniu 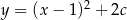 leży na prostej o równaniu
leży na prostej o równaniu 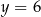 . Wtedy
. Wtedy
A) 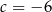 B)
B) 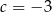 C)
C) 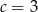 D)
D) 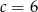
Liczba 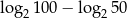 jest równa
jest równa
A) 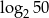 B) 1 C) 2 D)
B) 1 C) 2 D) 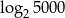
Wielomian 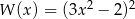 jest równy wielomianowi
jest równy wielomianowi
A) 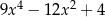 B)
B) 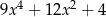 C)
C) 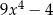 D)
D) 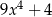
Z prostokąta 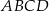 o obwodzie 30 wycięto trójkąt równoboczny
o obwodzie 30 wycięto trójkąt równoboczny  o obwodzie 15 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 15 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
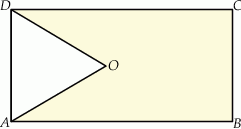
A) 25 B) 30 C) 35 D) 40
Liczby 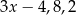 w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
A) 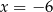 B)
B) 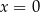 C)
C) 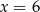 D)
D) 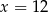
Punkt 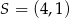 jest środkiem odcinka
jest środkiem odcinka 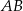 , gdzie
, gdzie 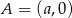 i
i 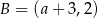 . Wówczas
. Wówczas
A) 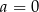 B)
B) 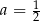 C)
C) 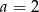 D)
D) 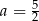
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 5?
A) 90 B) 100 C) 180 D) 200
Punkt 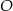 jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy 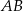 (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
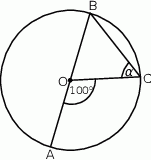
A) 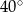 B)
B) 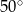 C)
C) 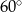 D)
D) 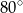
Najdłuższa przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 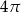 B)
B) 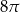 C)
C) 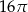 D)
D) 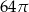
Pole równoległoboku o bokach długości 4 i 12 oraz kącie ostrym 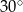 jest równe
jest równe
A) 24 B) 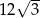 C) 12 D)
C) 12 D) 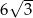
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wtedy liczba wszystkich jego wierzchołków jest równa
A) 6 B) 8 C) 12 D) 16
Objętość walca o wysokości 8 jest równa 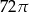 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Liczby 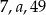 w podanej kolejności tworzą ciąg arytmetyczny. Wtedy
w podanej kolejności tworzą ciąg arytmetyczny. Wtedy  jest równe
jest równe
A) 14 B) 21 C) 28 D) 42
Ciąg 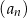 jest określony wzorem
jest określony wzorem 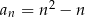 , dla
, dla 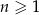 . Który wyraz tego ciągu jest równy 6?
. Który wyraz tego ciągu jest równy 6?
A) drugi B) trzeci C) szósty D) trzydziesty
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania pięciu oczek jest równe
A)  B)
B) 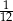 C)
C) 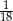 D)
D) 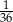
Kąt  jest ostry i
jest ostry i 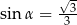 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 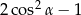 jest równa
jest równa
A) 0 B) 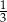 C)
C)  D) 1
D) 1
Na rysunku przedstawiono wykres funkcji 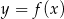 .
.
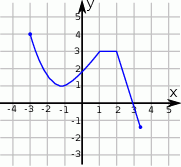
Największa wartość funkcji 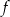 w przedziale
w przedziale 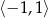 jest równa
jest równa
A) 4 B) 3 C) 2 D) 1
Zadania otwarte
Rozwiąż nierówność 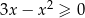 .
.
Rozwiąż równanie 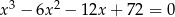 .
.
Kąt  jest ostry i
jest ostry i 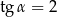 . Oblicz
. Oblicz 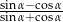 .
.
W tabeli zestawiono oceny z matematyki uczniów klasy 3A na koniec semestru.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 0 | 4 | 9 | 13 |  | 1 |
Średnia arytmetyczna tych ocen jest równa 3,6. Oblicz liczbę  ocen bardzo dobrych (5) z matematyki wystawionych na koniec semestru w tej klasie.
ocen bardzo dobrych (5) z matematyki wystawionych na koniec semestru w tej klasie.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 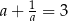 , to
, to 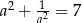 .
.
Długość krawędzi sześcianu jest o 2 krótsza od długości jego przekątnej. Oblicz długość przekątnej tego sześcianu.
Dane są dwie prostokątne działki. Działka pierwsza ma powierzchnię równą 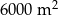 . Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o
. Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o 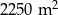 . Oblicz wymiary pierwszej działki.
. Oblicz wymiary pierwszej działki.
Punkty 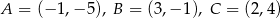 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 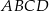 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Objętość ostrosłupa prawidłowego trójkątnego 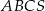 (tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę 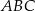 tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.