/Szkoła średnia/Zadania maturalne/Matura 2013/Matura
Egzamin Maturalny
z Matematyki poziom rozszerzony 10 maja 2013 Czas pracy: 180 minut
Rozwiąż nierówność 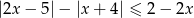 .
.
Trapez równoramienny 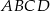 o podstawach
o podstawach 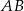 i
i 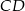 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 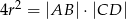 .
.
Oblicz, ile jest liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie trzy razy cyfra 0 i dokładnie raz występuje cyfra 5.
Rozwiąż równanie 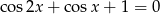 dla
dla 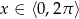 .
.
Ciąg liczbowy 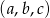 jest arytmetyczny i
jest arytmetyczny i 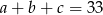 , natomiast ciąg
, natomiast ciąg 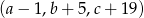 jest geometryczny. Oblicz
jest geometryczny. Oblicz 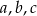 .
.
Wyznacz wszystkie wartości parametru 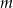 , dla których równanie
, dla których równanie 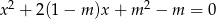 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 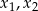 spełniające warunek
spełniające warunek 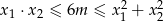 .
.
Prosta o równaniu 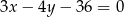 przecina okrąg o środku
przecina okrąg o środku 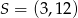 w punktach
w punktach 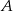 i
i 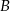 . Długość odcinka
. Długość odcinka 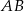 jest równa 40. Wyznacz równanie tego okręgu.
jest równa 40. Wyznacz równanie tego okręgu.
Reszta z dzielenia wielomianu 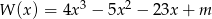 przez dwumian
przez dwumian 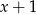 jest równa 20. Oblicz wartość współczynnika
jest równa 20. Oblicz wartość współczynnika 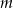 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Dany jest trójkąt 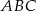 , w którym
, w którym 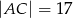 i
i 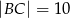 . Na boku
. Na boku 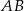 leży punkt
leży punkt 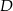 taki, że
taki, że 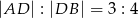 oraz
oraz 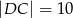 . Oblicz pole trójkąta
. Oblicz pole trójkąta 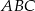 .
.
W ostrosłupie 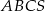 podstawa
podstawa 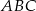 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Krawędź
. Krawędź 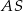 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 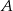 od ściany
od ściany 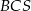 jest równa
jest równa 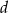 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy 60 .
Na rysunku przedstawiony jest fragment wykresu funkcji logarytmicznej 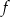 określonej wzorem
określonej wzorem 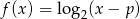 .
.
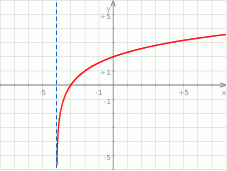
- Podaj wartość
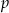 .
. - Narysuj wykres funkcji określonej wzorem
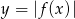 .
. - Podaj wszystkie wartości parametru
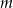 , dla których równanie
, dla których równanie 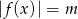 ma dwa rozwiązania o przeciwnych znakach.
ma dwa rozwiązania o przeciwnych znakach.

