/Szkoła średnia/Zadania maturalne/Matura 2014
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 5 kwietnia 2014 Czas pracy: 180 minut
Rozwiąż nierówność 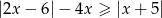 .
.
Ciąg 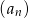 jest określony wzorem
jest określony wzorem 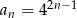 , gdzie
, gdzie 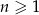 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 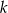 , dla których iloczyn
, dla których iloczyn 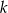 początkowych wyrazów ciągu
początkowych wyrazów ciągu 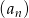 jest równy
jest równy 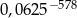 .
.
Wykaż, że jeżeli 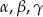 są kątami ostrymi i
są kątami ostrymi i 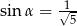 ,
, 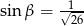 ,
, 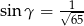 to
to 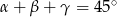 .
.
Wyznacz wszystkie wartości parametru 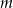 , dla których równanie
, dla których równanie 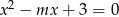 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 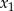 i
i 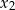 takie, że
takie, że 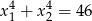 .
.
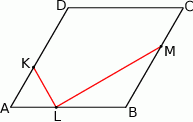
Na bokach 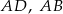 i
i 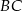 rombu
rombu 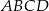 wybrano punkty
wybrano punkty 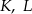 i
i 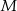 w ten sposób, że
w ten sposób, że 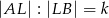 oraz
oraz 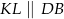 ,
, 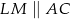 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 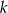 , dla których pole pięciokąta
, dla których pole pięciokąta 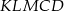 stanowi
stanowi 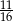 pola rombu.
pola rombu.
Wyznacz współrzędne punktu 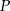 leżącego na prostej o równaniu
leżącego na prostej o równaniu 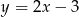 , którego suma kwadratów odległości od punktów
, którego suma kwadratów odległości od punktów 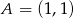 i
i 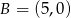 jest najmniejsza.
jest najmniejsza.
Rozwiąż układ równań 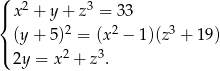
Reszty z dzielenia wielomianu 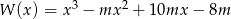 przez dwumiany
przez dwumiany 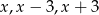 są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru
są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru 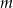 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Kąty ostre trójkąta 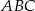 o polu
o polu 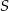 mają miary
mają miary 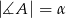 ,
, 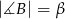 . Oblicz długości boków
. Oblicz długości boków 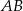 i
i 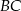 tego trójkąta.
tego trójkąta.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 4.
W ostrosłupie prawidłowym trójkątnym długość krawędzi podstawy jest równa  i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.

