/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 26 kwietnia 2014 Czas pracy: 170 minut
Zadania zamknięte
Badając pewien roztwór stwierdzono, że zawiera on 0,06 g chloru, co stanowi 0,04% masy roztworu. Jaka była masa roztworu?
A) 1,5 kg B) 15 g C) 150 g D) 1,5 g
Liczba 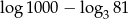 jest równa
jest równa
A) 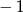 B)
B) 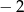 C) 0 D) 1
C) 0 D) 1
Suma przedziałów 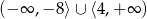 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 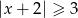 B)
B) 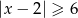 C)
C) 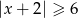 D)
D) 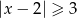
Jeżeli 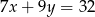 i
i 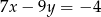 to
to
A) 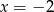 B)
B) 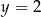 C)
C) 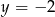 D)
D) 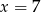
Wyrażenie 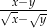 jest równe
jest równe
A) 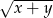 B)
B) 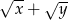 C)
C) 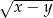 D)
D) 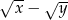
Wiadomo, że 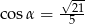 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia 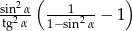 jest równa:
jest równa:
A) 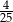 B)
B) 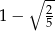 C)
C) 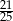 D)
D) 
Wierzchołkiem paraboli o równaniu 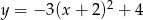 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 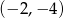 B)
B) 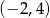 C)
C) 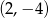 D)
D) 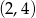
Dla każdych liczb rzeczywistych 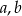 wyrażenie
wyrażenie 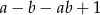 jest równe
jest równe
A) 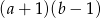 B)
B) 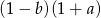 C)
C) 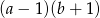 D)
D) 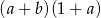
Suma liczb całkowitych dodatnich spełniających nierówność 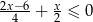 jest równa
jest równa
A) 1 B) 3 C) 0 D) 6
Liczba 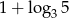 jest równa:
jest równa:
A) 2 B) 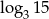 C)
C) 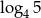 D)
D) 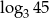
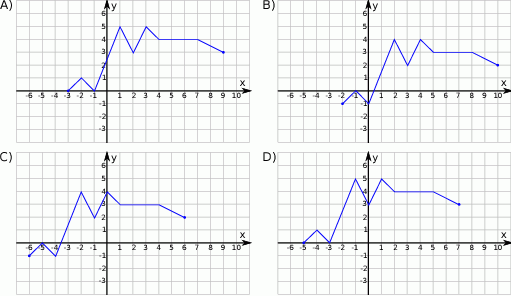
Rysunek przedstawia wykres funkcji 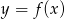 .
.
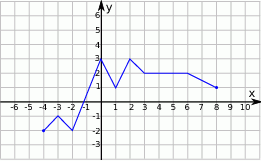
Wskaż wykres funkcji 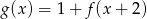 .
.
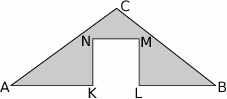
Z trójkąta 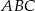 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 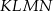 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
A) 65 B) 60 C) 75 D) 70
Cztery liczby dodatnie 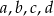 w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby
w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby 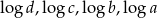 (w podanej kolejności) tworzą
(w podanej kolejności) tworzą
A) ciąg geometryczny o ilorazie 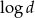
B) ciąg arytmetyczny o różnicy 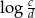
C) ciąg arytmetyczny o różnicy 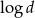
D) ciąg arytmetyczny o różnicy 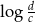
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 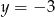 i wewnętrznie styczne do okręgu
i wewnętrznie styczne do okręgu 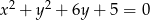 ?
?
A) 1 B) 2 C) 3 D) 4
Liczba niewymiernych pierwiastków równania 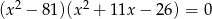 jest równa
jest równa
A) 0 B) 2 C) 3 D) 4
Punkt 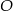 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 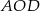 ma miarę
ma miarę
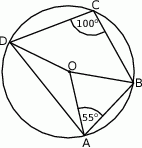
A) 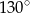 B)
B) 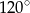 C)
C) 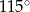 D)
D) 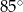
Liczba 5 jest czwartym wyrazem ciągu:
A) 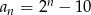 B)
B) 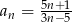 C)
C) 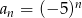 D)
D) 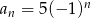
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie
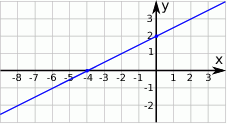
A) 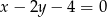 B)
B) 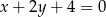 C)
C) 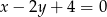 D)
D) 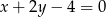
Zbiór punktów wspólnych kuli i prostej może być
A) zbiorem dwuelementowym B) zbiorem jednoelementowym C) okręgiem D) kołem
Objętość walca o wysokości 4 jest równa 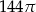 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Ania otrzymała z pięciu sprawdzianów z matematyki następujące oceny: 5, 2, 3, 2, 5. Po kolejnych dwóch sprawdzianach średnia ocen Ani ze wszystkich sprawdzianów wyniosła 4. Jakie oceny mogła otrzymać Ania z ostatnich dwóch sprawdzianów?
A) 4 i 5 B) 5 i 5 C) 6 i 6 D) 5 i 6
Losujemy jeden bok i jeden wierzchołek kwadratu. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest końcem wylosowanego odcinka jest równe
A) 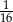 B)
B) 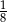 C)
C) 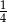 D)
D) 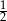
Liczba 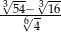 jest równa
jest równa
A) 2 B) 1 C) 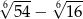 D)
D) 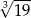
Kąt  jest kątem ostrym i
jest kątem ostrym i 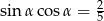 . Wówczas wyrażenie
. Wówczas wyrażenie 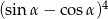 jest równe
jest równe
A) 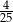 B)
B) 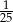 C)
C) 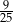 D)
D) 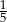
Punkt 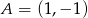 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 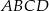 , którego bok
, którego bok 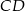 zawiera się w prostej
zawiera się w prostej 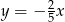 . Podstawa
. Podstawa 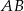 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 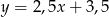 B)
B) 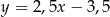 C)
C) 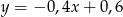 D)
D) 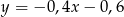
Zadania otwarte
Rozwiąż równanie 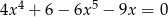 .
.
Wykaż, że liczba 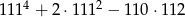 jest dzielnikiem liczby
jest dzielnikiem liczby
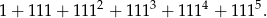
Z danego wykresu funkcji 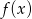 odczytaj
odczytaj
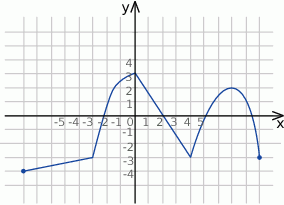
- zbiór wartości funkcji
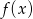 ;
; - rozwiązania równania
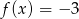 ;
; - maksymalne przedziały, na których funkcja
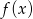 jest rosnąca.
jest rosnąca.
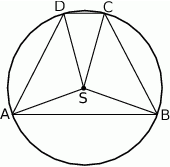
Punkt 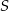 jest środkiem okręgu opisanego na trapezie równoramiennym
jest środkiem okręgu opisanego na trapezie równoramiennym 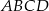 . Kąt
. Kąt 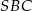 jest dwa razy większy od kąta
jest dwa razy większy od kąta 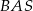 , a kąt
, a kąt 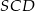 jest dwa razy większy od kąta
jest dwa razy większy od kąta 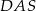 . Oblicz kąty trapezu
. Oblicz kąty trapezu 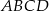 .
.
Kwadrat odchylenia standardowego danych: 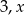 jest równy 1. Oblicz
jest równy 1. Oblicz  .
.
Dane są niezerowe liczby wymierne 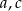 takie, że funkcja
takie, że funkcja 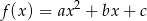 ma miejsce zerowe będące liczbą wymierną. Wykaż, że
ma miejsce zerowe będące liczbą wymierną. Wykaż, że 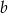 jest liczbą wymierną.
jest liczbą wymierną.
Oblicz, ile jest liczb naturalnych trzycyfrowych, które są podzielne przez 5, i których zapis składa się z 3 różnych cyfr.
Oblicz pole równoległoboku 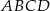 o wierzchołkach
o wierzchołkach 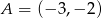 ,
, 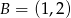 ,
, 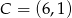 ,
, 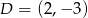 .
.
Podstawą graniastosłupa 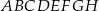 o objętości 162 jest prostokąt
o objętości 162 jest prostokąt 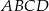 (zobacz rysunek), którego przekątna tworzy z jego bokiem kąt
(zobacz rysunek), którego przekątna tworzy z jego bokiem kąt 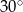 . Przekątna
. Przekątna 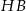 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 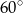 stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.