/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 5 kwietnia 2014 Czas pracy: 170 minut
Zadania zamknięte
Która z liczb jest największa?
A) 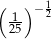 B)
B) 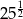 C)
C) 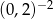 D)
D) 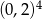
Gdy do 50% liczby 73 dodamy 73% liczby 50, to otrzymamy
A) 1 B) 73 C) 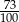 D) 100
D) 100
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 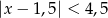 B)
B) 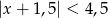 C)
C) 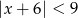 D)
D) 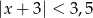
Wykres funkcji kwadratowej 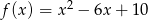 powstaje z wykresu funkcji
powstaje z wykresu funkcji 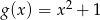 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Prosta o równaniu  jest nachylona do osi
jest nachylona do osi 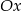 pod kątem
pod kątem
A) 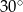 B)
B) 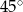 C)
C) 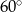 D)
D) 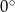
Liczby rzeczywiste 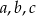 spełniają warunki:
spełniają warunki: 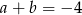 ,
, 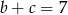 i
i 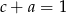 . Wtedy suma
. Wtedy suma 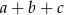 jest równa
jest równa
A) 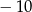 B) 8 C) 4 D) 2
B) 8 C) 4 D) 2
Dla każdego kąta ostrego  wyrażenie
wyrażenie 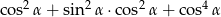 jest równe
jest równe
A) 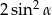 B)
B) 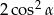 C) 1 D) 2
C) 1 D) 2
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
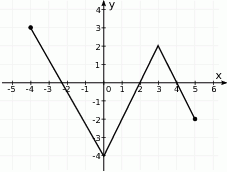
A) 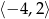 B)
B) 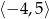 C)
C) 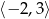 D)
D) 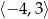
Dla każdej liczby rzeczywistej  , wyrażenie
, wyrażenie 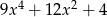 jest równe
jest równe
A) 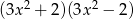 B)
B) 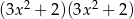 C)
C) 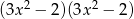 D)
D) 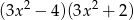
Liczba 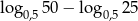 jest równa
jest równa
A) 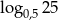 B) 1 C)
B) 1 C) 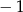 D)
D) 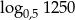
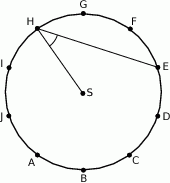
Punkty 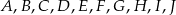 dzielą okrąg o środku
dzielą okrąg o środku 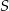 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 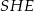 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 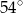 B)
B) 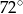 C)
C) 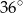 D)
D) 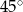
Na rysunku poniżej przedstawiony jest fragment wykresu funkcji liniowej 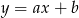 .
.
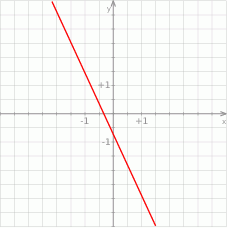
Jakie nierówności spełniają współczynniki  i
i 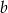 ?
?
A) 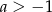 i
i 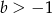 B)
B) 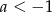 i
i 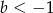 C)
C) 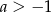 i
i 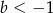 D)
D) 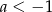 i
i 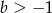
Nierówność 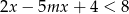 jest spełniona przez każdą liczbę rzeczywistą jeżeli
jest spełniona przez każdą liczbę rzeczywistą jeżeli
A) 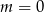 B)
B) 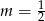 C)
C) 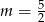 D)
D) 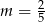
Punkt 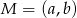 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 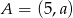 i
i 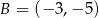 . Wówczas
. Wówczas
A) 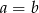 B)
B) 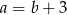 C)
C) 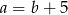 D)
D) 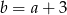
Stosunek długości trzech krawędzi prostopadłościanu o objętości 240 jest równy 2:3:5. Pole powierzchni tego prostopadłościanu jest równe:
A) 124 B) 248 C) 496 D) 62
Ciąg 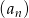 określony dla
określony dla 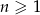 jest arytmetyczny oraz
jest arytmetyczny oraz 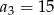 i
i 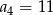 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 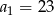 B)
B) 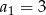 C)
C) 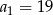 D)
D) 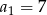
Kwotę 1000 zł wpłacamy do banku na 3 lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa procentowa wynosi 8%. Po trzech latach otrzymamy kwotę
A) 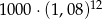 B)
B) 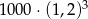 C)
C) 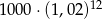 D)
D) 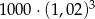
Pole równoległoboku o bokach długości 6 i 10 oraz kącie ostrym 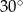 jest równe
jest równe
A) 60 B) 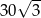 C) 30 D)
C) 30 D) 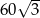
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 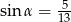 . Bok
. Bok 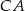 tego trójkąta ma długość:
tego trójkąta ma długość:
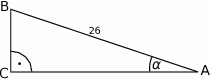
A) 10 B) 24 C) 12 D) 5
Odległość między środkami okręgów o równaniach 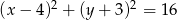 oraz
oraz 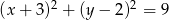 jest równa
jest równa
A) 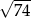 B)
B) 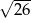 C)
C) 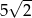 D)
D) 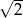
Pole powierzchni bocznej stożka wynosi 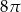 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 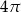 B)
B) 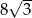 C)
C) 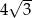 D)
D) 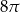
Dany jest ciąg 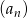 o wyrazie ogólnym
o wyrazie ogólnym 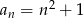 , gdzie
, gdzie 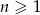 . Wówczas
. Wówczas
A) 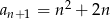 B)
B) 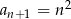 C)
C) 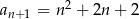 D)
D) 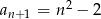
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwa orły jest równe
A) 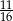 B)
B)  C)
C) 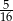 D)
D) 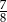
Zadania otwarte
Rozwiąż nierówność 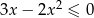 .
.
Kąt  jest ostry oraz
jest ostry oraz 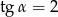 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 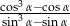 .
.
Nieskończony ciąg geometryczny 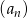 jest określony wzorem
jest określony wzorem 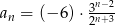 , dla
, dla 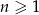 . Oblicz iloraz
. Oblicz iloraz 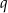 tego ciągu.
tego ciągu.
Liczby  i
i 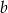 są nieparzyste i dają przy dzieleniu przez 4 różne reszty. Wykaż, że suma kwadratów tych liczb nie jest podzielna przez 4.
są nieparzyste i dają przy dzieleniu przez 4 różne reszty. Wykaż, że suma kwadratów tych liczb nie jest podzielna przez 4.
Wiadomo, że 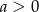 i
i 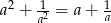 . Wykaż, że
. Wykaż, że 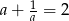 .
.
Oblicz sumę wszystkich liczb trzycyfrowych, których cyfra jedności jest równa 3 lub 8.
Punkt 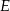 jest środkiem boku
jest środkiem boku 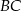 równoległoboku
równoległoboku 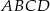 , a odcinek
, a odcinek 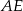 przecina przekątną
przecina przekątną 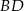 w punkcie
w punkcie 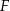 . Wykaż, że
. Wykaż, że 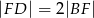 .
.
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 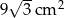 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 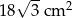 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W rombie 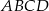 dane są
dane są 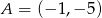 i punkt przecięcia przekątnych
i punkt przecięcia przekątnych 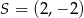 . Wierzchołek
. Wierzchołek 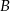 leży na prostej
leży na prostej 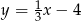 . Oblicz współrzędne pozostałych wierzchołków rombu.
. Oblicz współrzędne pozostałych wierzchołków rombu.
Grupa znajomych postanowiła raz w tygodniu wynajmować salę gimnastyczną. Jednorazowa opłata za wynajęcie sali wynosiła 240 zł i podzielono ją na równe części tak, aby każdy ze znajomych płacił tyle samo. W drugim tygodniu do grupy dołączyły jeszcze dwie osoby i wówczas opłata przypadająca na każdego ze znajomych zmniejszyła się o 4 złote. Ile osób liczyła ta grupa w pierwszym tygodniu użytkowania sali?

