/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 29 marca 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 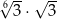 jest równa
jest równa
A) 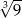 B)
B) 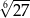 C)
C) 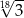 D)
D) 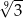
Ilustracją graficzną zbioru rozwiązań nierówności 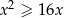 jest przedział:
jest przedział:

Liczby  i
i 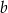 są dodatnie oraz 14% liczby
są dodatnie oraz 14% liczby  jest równe 21% liczby
jest równe 21% liczby 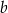 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 103% liczby 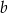 B) 125% liczby
B) 125% liczby 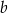 C) 150% liczby
C) 150% liczby 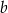 D) 153% liczby
D) 153% liczby 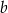
Liczba ![[ ] √ - log3 log64(log 39)](https://img.zadania.info/zes/0082808/HzesT16x.gif) jest równa
jest równa
A) 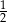 B)
B) 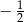 C) 1 D)
C) 1 D) 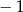
Funkcja 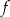 jest określona wzorem
jest określona wzorem 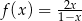 dla
dla 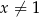 . Wartość funkcji
. Wartość funkcji 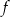 dla argumentu
dla argumentu 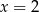 jest równa
jest równa
A) 2 B) 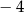 C) 4 D)
C) 4 D) 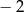
Wykres funkcji liniowej 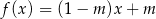 przechodzi przez I, III i IV ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy
przechodzi przez I, III i IV ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy
A) 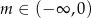 B)
B) 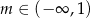 C)
C) 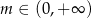 D)
D) 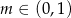
Liczbami spełniającymi równanie 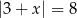 są
są
A) 11 i 5 B) 3 i 8 C) 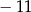 i 5 D)
i 5 D) 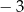 i 8
i 8
Na rysunku przedstawiono wykres funkcji 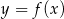 .
.
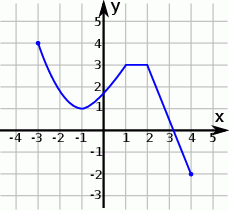
Najmniejsza wartość funkcji 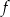 w przedziale
w przedziale 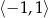 jest równa
jest równa
A) 3 B) 1 C) 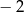 D)
D) 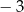
Wierzchołek paraboli o równaniu 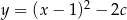 leży na prostej o równaniu
leży na prostej o równaniu 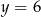 . Wtedy
. Wtedy
A) 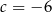 B)
B) 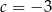 C)
C) 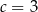 D)
D) 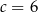
Na rysunku przedstawiony jest wykres funkcji 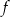 .
.
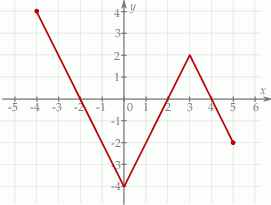
Maksymalnym zbiorem, w którym funkcja 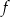 przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 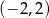 B)
B) 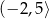 C)
C) 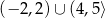 D)
D) 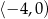
Prosta o równaniu 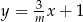 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 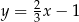 . Stąd wynika, że
. Stąd wynika, że
A) 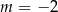 B)
B) 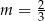 C)
C) 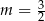 D)
D) 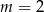
Iloczyn wielomianów 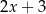 oraz
oraz 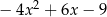 jest równy
jest równy
A) 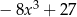 B)
B) 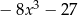 C)
C) 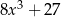 D)
D) 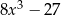
Liczby 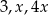 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 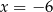 B)
B) 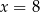 C)
C) 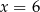 D)
D) 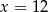
Pole rombu o boku równym 6 cm i kącie rozwartym wynoszącym 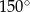 wynosi
wynosi
A) 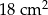 B)
B) 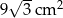 C)
C) 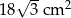 D)
D) 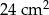
Kąt  jest ostry i
jest ostry i 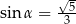 . Wartość wyrażenia
. Wartość wyrażenia 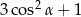 jest równa
jest równa
A)  B)
B) 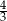 C)
C)  D)
D) 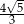
Średnice 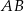 i
i 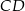 okręgu o środku
okręgu o środku 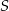 przecinają się pod kątem
przecinają się pod kątem 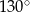 (tak jak na rysunku).
(tak jak na rysunku).
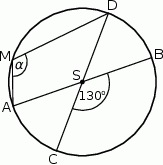
Miara kąta  jest równa
jest równa
A) 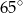 B)
B) 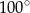 C)
C) 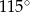 D)
D) 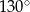
Najdłuższa przekątna sześciokąta foremnego ma długość 6. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 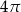 B)
B) 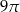 C)
C) 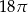 D)
D) 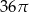
Punkt 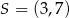 jest środkiem odcinka
jest środkiem odcinka 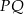 , gdzie
, gdzie 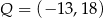 . Zatem punkt
. Zatem punkt 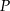 ma współrzędne
ma współrzędne
A) 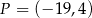 B)
B) 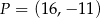 C)
C) 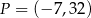 D)
D) 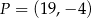
Liczba 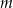 , dla której rozwiązaniem równania
, dla której rozwiązaniem równania 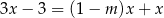 jest
jest 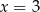 wynosi
wynosi
A) 3 B) 2 C) 1 D) 0
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 67035 B) 49629 C) 17022 D) 16919
Ciąg 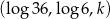 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 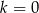 B)
B) 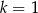 C)
C) 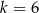 D)
D) 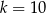
W ciągu geometrycznym piąty wyraz jest równy  , a szósty wyraz jest równy
, a szósty wyraz jest równy 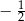 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 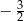 D)
D) 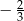
Wyniki sprawdzianu z geografii są przedstawione na diagramie
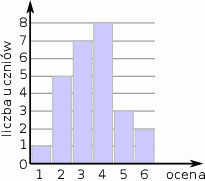
Ile osób uzyskało ocenę wyższą od średniej ocen z tego sprawdzianu?
A) 5 B) 8 C) 20 D) 13
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Pole powierzchni całkowitej tego graniastosłupa jest równe 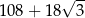 . Długość krawędzi tego graniastosłupa jest równa
. Długość krawędzi tego graniastosłupa jest równa
A) 12 B) 10 C) 9 D) 6
Liczba wszystkich sposobów utworzenia liczb trzycyfrowych o różnych cyfrach ze zbioru 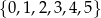 jest równa
jest równa
A) 120 B) 100 C) 60 D) 60
Zadania otwarte
Rozwiąż równanie 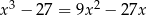 .
.
Rozwiąż nierówność 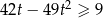 .
.
Kąt  jest ostry i
jest ostry i 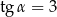 . Oblicz
. Oblicz 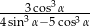 .
.
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których cyfra jedności jest o 4 mniejsza od cyfry setek?
Wykaż, że dla dowolnej liczby rzeczywistej 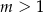 istnieje dokładnie jedna liczba rzeczywista
istnieje dokładnie jedna liczba rzeczywista  taka, że
taka, że
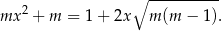
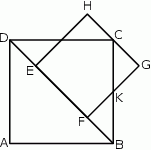
Bok 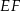 kwadratu
kwadratu 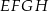 zawiera się w przekątnej
zawiera się w przekątnej 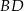 kwadratu
kwadratu 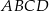 , a punkt
, a punkt 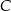 jest środkiem odcinka
jest środkiem odcinka 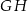 . Odcinki
. Odcinki 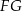 i
i 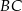 przecinają się w punkcie
przecinają się w punkcie 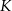 . Wykaż, że
. Wykaż, że 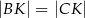 .
.
Liczby 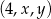 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zwiększymy o 1, a liczbę
zwiększymy o 1, a liczbę 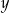 zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz
zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz  i
i 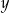 .
.
Dwa miasta łączy droga o długości 448 kilometrów. Samochód 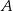 przebył tę trasę w czasie o 40 minut krótszym niż samochód
przebył tę trasę w czasie o 40 minut krótszym niż samochód 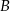 . Średnia prędkość samochodu
. Średnia prędkość samochodu 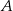 na tej trasie była o 12 km/h większa od średniej prędkości samochodu
na tej trasie była o 12 km/h większa od średniej prędkości samochodu 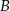 . Oblicz średnią prędkość każdego z tych samochodów na tej trasie.
. Oblicz średnią prędkość każdego z tych samochodów na tej trasie.
Objętość ostrosłupa prawidłowego trójkątnego 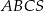 (tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę  tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.