/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna/CKE, OKE, CEN

Lubelska próba przed maturą
z matematyki poziom rozszerzony 25 lutego 2014 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

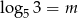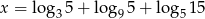Wiadomo, że log53 = m . Oblicz liczbę x = log3 5+ lo g95 + log5 15 .

Zadanie 2
(4 pkt)

Sporządź wykres funkcji 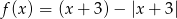f (x) = (x + 3) − |x+ 3| . Podaj miejsca zerowe funkcji, oraz przedziały monotoniczności.

Zadanie 3
(3 pkt)

Wyznacz zbiór wartości funkcji określonej wzorem: 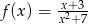f(x) = xx+2+37 dla x ∈ R .

Zadanie 4
(3 pkt)

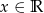Dwie dowolne liczby rzeczywiste i ich suma tworzą ciąg arytmetyczny (niekoniecznie w takiej kolejności). Wykaż, że jedna z tych liczb jest dwukrotnością drugiej liczby lub, że liczby te są liczbami przeciwnymi.

Zadanie 5
(4 pkt)

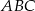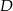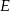Dany jest trójkąt prostokątny równoramienny ABC . Punkty D i E dzielą przeciwprostokątną 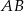AB na trzy odcinki równej długości. Oblicz cosinus kąta DCE .

Zadanie 6
(6 pkt)

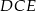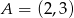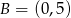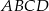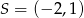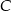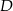Odcinek o końcach A = (2,3) i B = (0,5) jest podstawą trapezu ABCD . Druga podstawa o środku w punkcie S = (− 2,1) jest dwa razy dłuższa od podstawy AB. Wyznacz współrzędne wierzchołków C i D . Oblicz pole tego trapezu.

Zadanie 7
(3 pkt)

Wykaż, że jeżeli kąty trójkąta: 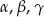α,β ,γ spełniają równanie 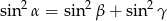sin 2α = sin2 β + sin2γ to trójkąt jest prostokątny.

Zadanie 8
(5 pkt)

Przekrój ostrosłupa prawidłowego czworokątnego zawierającego przekątną podstawy oraz wierzchołek ostrosłupa jest trójkątem równobocznym o polu 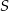S . Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.

Zadanie 9
(5 pkt)

Rozwiąż równanie: 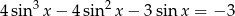3 2 4 sin x − 4sin x− 3sin x = − 3 w przedziale ⟨0,2π ⟩ .

Zadanie 10
(6 pkt)

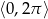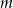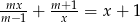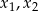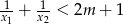Dla jakich wartości parametru m równanie mx m +1 m-−1 + --x- = x + 1 ma dwa różne pierwiastki x1,x 2 , spełniające warunek 1-+ 1-< 2m + 1 x1 x2 .

Zadanie 11
(4 pkt)

Dla jakich wartości 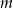m reszta z dzielenia wielomianu 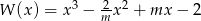W (x) = x3 − 2mx 2 + mx − 2 przez dwumian 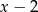x − 2 jest mniejsza lub równa 6?

Zadanie 12
(3 pkt)

Zamek szyfrowy składa się z 5 tarcz. Na każdej z tarcz znajduje się 6 cyfr. Zamek otwiera kombinacja cyfr podana w odpowiedniej kolejności. (istotne są cyfry na tarczach oraz kolejność ustawiania tarcz). Jakie jest prawdopodobieństwo otworzenia zamka przy losowym ustawieniu tarcz?

Rozwiąż on-line Arkusz Wersja PDF
Rozwiązania