/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa I 25 lutego 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 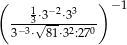 jest równa
jest równa
A) 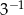 B)
B) 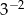 C)
C) 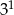 D)
D) 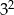
Liczba 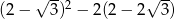 jest równa
jest równa
A) 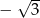 B) 3 C)
B) 3 C) 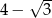 D)
D) 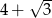
Liczbą odwrotną do liczby 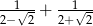 jest liczba
jest liczba
A) 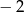 B) 2 C)
B) 2 C) 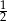 D)
D) 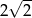
Cenę książki obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 10%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 25% B) 28% C) 29% D) 30%
Wartość liczbowa wyrażenia 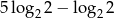 jest równa
jest równa
A) 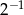 B)
B) 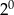 C)
C) 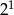 D)
D) 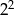
Liczba 5 jest pierwiastkiem wielomianu 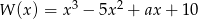 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 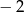 B)
B) 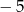 C) 2 D) 5
C) 2 D) 5
Rozwiązaniem nierówności 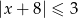 jest zbiór
jest zbiór
A) 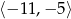 B)
B) 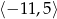 C)
C) 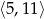 D)
D) 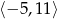
Długość odcinka 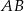 o końcach w punktach
o końcach w punktach 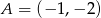 i
i 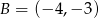 jest równa
jest równa
A) 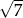 B)
B) 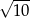 C)
C) 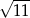 D)
D) 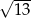
W trójkącie równoramiennym ramię ma długość 5, a kąt ostry przy podstawie jest równy  . Wysokość poprowadzona na podstawę trójkąta wynosi
. Wysokość poprowadzona na podstawę trójkąta wynosi
A) 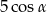 B)
B) 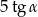 C)
C) 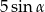 D)
D) 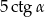
Prosta prostopadła do prostej o równaniu 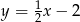 i przechodząca przez punkt
i przechodząca przez punkt 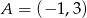 ma równanie
ma równanie
A) 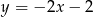 B)
B) 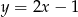 C)
C) 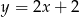 D)
D) 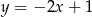
Rozwiązaniem równania 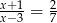 jest liczba
jest liczba
A) 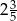 B)
B) 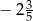 C)
C) 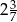 D)
D) 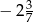
Zbiorem rozwiązań nierówności 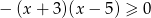 jest
jest
A) 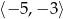 B)
B) 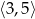 C)
C) 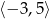 D)
D) 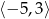
Największą liczbą całkowitą należącą do zbioru rozwiązań nierówności 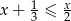 jest
jest
A) 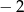 B)
B) 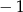 C) 1 D) 2
C) 1 D) 2
Funkcja liniowa 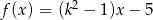 jest malejąca dla
jest malejąca dla
A) 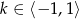 B)
B) 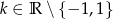 C)
C) 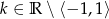 D)
D) 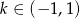
Najmniejsza wartość funkcji 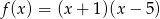 wynosi
wynosi
A) 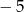 B) 5 C)
B) 5 C) 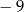 D)
D) 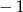
Suma długości krawędzi sześcianu jest równa 60 cm. Długość przekątnej tego sześcianu wynosi
A) 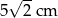 B)
B) 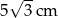 C)
C) 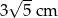 D)
D) 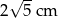
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 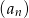 , w którym
, w którym 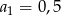 oraz
oraz 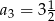 jest równa
jest równa
A) 295 B) 298 C) 305 D) 308
Na diagramie podano wzrost uczniów klasy I w pewnym liceum.
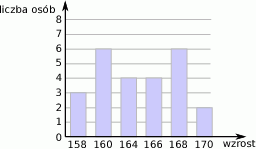
Mediana wszystkich wyników jest równa
A) 163 B) 164 C) 165 D) 166
Liczby 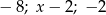 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  może być równa
może być równa
A) 4 B) 6 C) 7 D) 8
Kąt  jest kątem ostrym w trójkącie prostokątnym i
jest kątem ostrym w trójkącie prostokątnym i 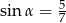 . Wówczas
. Wówczas
A) 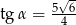 B)
B) 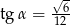 C)
C) 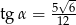 D)
D) 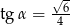
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 17 B) 18 C) 19 D) 20
Dany jest okrąg o środku 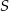 i promieniu
i promieniu  , długość łuku
, długość łuku 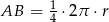 (patrz rysunek).
(patrz rysunek).
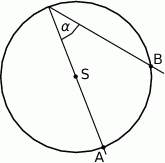
Miara kąta  jest równa
jest równa
A) 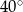 B)
B) 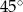 C)
C) 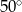 D)
D) 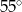
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano pikową damę lub kierowego waleta?
A) 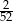 B)
B) 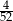 C)
C) 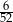 D)
D) 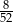
Zadania otwarte
Wykaż, że ciąg o wzorze ogólnym 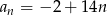 , gdzie
, gdzie 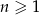 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Dla jakich argumentów  , funkcja
, funkcja 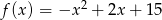 przyjmuje wartości dodatnie?
przyjmuje wartości dodatnie?
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 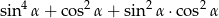 jest stała.
jest stała.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną monetą. Jakie jest prawdopodobieństwo, że wylosujemy co najmniej dwa razy orła?
Rozwiąż równanie 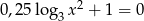 .
.
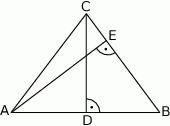
Oblicz pole trójkąta równoramiennego 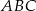 (patrz rysunek,
(patrz rysunek, 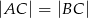 ), w którym wysokość
), w którym wysokość 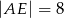 , a długość odcinka
, a długość odcinka 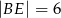 .
.
Dany jest prostokąt o polu 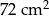 . Gdyby zwiększyć długość jednego z boków o 2 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.
. Gdyby zwiększyć długość jednego z boków o 2 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.
Dane są dwa punkty 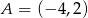 i
i 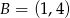 oraz prosta
oraz prosta 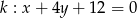 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 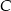 leżącego na prostej
leżącego na prostej 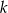 i tak samo odległego od punktów
i tak samo odległego od punktów 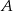 i
i 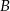 .
.
Objętość stożka jest równa 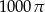 , a tworząca jest nachylona do podstawy pod kątem
, a tworząca jest nachylona do podstawy pod kątem 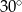 . Oblicz pole powierzchni bocznej tego stożka.
. Oblicz pole powierzchni bocznej tego stożka.

