/Gimnazjum/Egzamin gimnazjalny/Egzamin 2014
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 12 kwietnia 2014 Czas pracy: 90 minut
Informacja do zadań 1 – 3
W tabeli przedstawiono informacje dotyczące półrocznej sprzedaży w pewnej firmie handlowej.
| Miesiąc | Wartość sprzedaży |
| 1 | 1500 zł |
| 2 | 800 zł |
| 3 | 2700 zł |
| 4 | 900 zł |
| 5 | 1200 zł |
| 6 | 900 zł |
Na którym diagramie poprawnie przedstawiono jak zmieniała się całkowita wartość sprzedaży od początku roku? Wybierz odpowiedź spośród podanych.
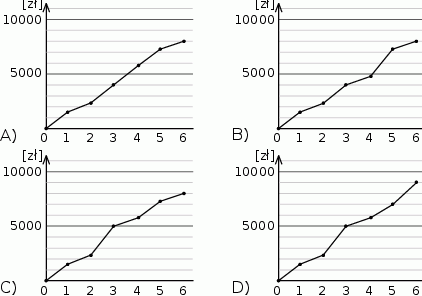
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Średnia miesięczna sprzedaż w tej firmie
A) wyniosła 1300 zł
B) była większa niż 1300 zł
C) wyniosła 666 zł
D) była mniejsza niż 600 zł
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sprzedaż w 1 kwartale była wyższa niż sprzedaż w 2 kwartale. | P | F |
| Sprzedaż była najniższa w 4 miesiącu. | P | F |
Cena brutto = cena netto + podatek VAT
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto laptopa jest równa 1200 zł, a cena brutto jest równa 1440 zł, to podatek VAT wynosi 22% ceny netto. | P | F |
| Jeżeli cena netto myszki komputerowej jest równa 36 zł, to cena tej myszki z 20% podatkiem VAT wynosi 43,20 zł. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Emil kolekcjonuje modele samochodów. Co trzeci z jego modeli to model samochodu terenowego, co czwarty to model ciężarówki, a pozostałe 20 modeli to modele samochodów osobowych. Emil ma w swojej kolekcji
A) 64 modele. B) 48 modeli. C) 36 modeli. D) 32 modele.
Dane są liczby: 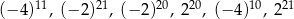 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych liczb jest więcej liczb dodatnich, niż ujemnych. | P | F |
Wśród podanych liczb są 3 liczby równe 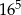 . . | P | F |
Tomek ma w skarbonce 156 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy mniej niż pięciozłotowych.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli przez  oznaczymy liczbę monet pięciozłotowych, a przez
oznaczymy liczbę monet pięciozłotowych, a przez 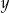 – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
– liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
A) 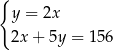 B)
B) 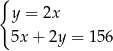 C)
C) 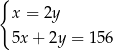 D)
D) 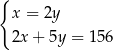
W pewnej piekarni wypieka się średnio 90 bochenków chleba dziennie. Z 3 kg mąki można upiec 5 bochenków chleba.
Ile co najmniej 20 kilogramowych worków mąki musi kupić właściciel piekarni, aby wystarczyło jej do wypieku chleba przez 7 dni? Wybierz odpowiedź spośród podanych.
A) 18 B) 19 C) 20 D) 6
W jakim stosunku można podzielić odcinek o długości 36 cm, aby z otrzymanych czterech odcinków móc zbudować czworokąt? Wybierz odpowiedź spośród podanych.
A) 1 : 1 : 2 : 4 B) 1 : 2 : 2 : 6 C) 2 : 3 : 4 : 8 D) 2 : 3 : 3 : 8
W pudełku było 15 kul białych i 5 czarnych. Dołożono jeszcze 10 kul białych i 20 czarnych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
Informacja do zadań 11 i 12
Ewa narysowała trójkąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego trójkąty rysowała w taki sposób, że środek podstawy rysowanego trójkąta był wierzchołkiem poprzedniego trójkąta (rysunek 2.).
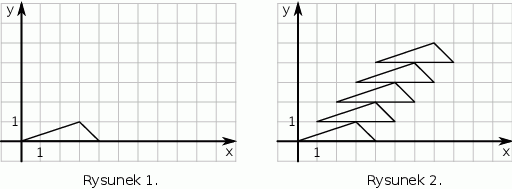
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Ewa narysowała w opisany sposób  trójkątów. Współrzędna
trójkątów. Współrzędna  górnego wierzchołka tego trójkąta jest równa
górnego wierzchołka tego trójkąta jest równa
A) 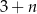 B)
B) 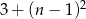 C)
C) 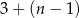 D)
D) 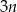
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Współrzędne środka podstawy ostatniego narysowanego trójkąta są równe 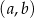 . Współrzędne środka podstawy w następnym trójkącie będą równe
. Współrzędne środka podstawy w następnym trójkącie będą równe
A) 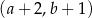 B)
B) 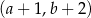 C)
C) 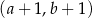 D)
D) 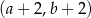
W układzie współrzędnych zaznaczono wierzchołki 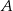 i
i 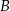 czworokąta
czworokąta  . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta.
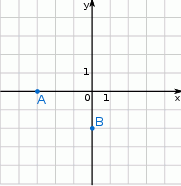
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Pole czworokąta  jest równe
jest równe
A) 9 B) 12 C) 18 D) 36
Dany jest trapez równoramienny  o podstawach długości 10 cm, 6 cm i ramieniu długości
o podstawach długości 10 cm, 6 cm i ramieniu długości 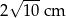 . Odcinek
. Odcinek 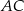 jest przekątną tego trapezu.
jest przekątną tego trapezu.
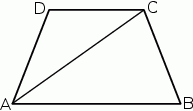
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 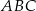 jest równoramienny. jest równoramienny. | P | F |
| Wysokość trapezu ma długość 5 cm. | P | F |
Na rysunku przedstawiono dwa trójkąty równoramienne.
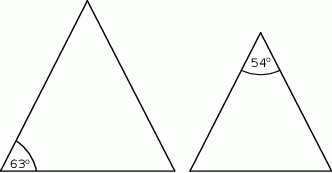
Czy te trójkąty są trójkątami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa trójkąty równoramienne są podobne. |
| B) | miary kątów jednego trójkąta są różne od miar kątów drugiego trójkąta. |
| C) | miary kątów jednego trójkąta są takie same jak miary kątów drugiego trójkąta. |
| D) | długości ramion jednego trójkąta są różne od długości ramion drugiego trójkąta. |
Kąt ostry rombu ma miarę 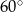 , a wysokość rombu jest równa
, a wysokość rombu jest równa 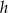 .
.
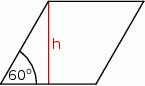
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole tego rombu można wyrazić wzorem
A) 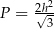 B)
B) 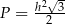 C)
C) 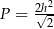 D)
D) 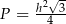
Jeden z kątów wewnętrznych trójkąta ma miarę  , drugi ma miarę o
, drugi ma miarę o 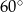 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Trójkąt ten jest
A) równoboczny. B) równoramienny. C) rozwartokątny. D) prostokątny.
Punkt 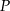 jest punktem wspólnym symetralnych boków
jest punktem wspólnym symetralnych boków 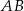 i
i 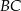 trójkąta
trójkąta  .
.
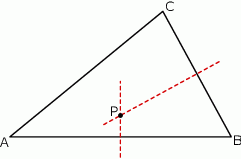
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Odległość punktu 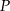 od wierzchołków od wierzchołków 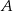 i i 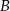 jest taka sama. jest taka sama. | P | F |
Odległość punktu 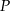 od wierzchołków od wierzchołków 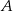 i i 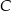 jest taka sama. jest taka sama. | P | F |
Który z poniższych rysunków nie może być siatką graniastosłupa prawidłowego trójkątnego? Wybierz odpowiedź spośród podanych.
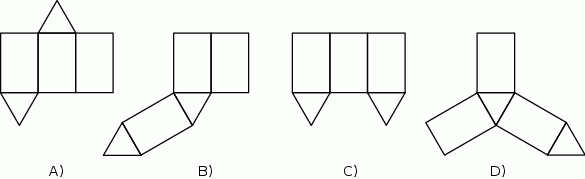
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Suma pól powierzchni 8 kul, z których każda ma promień 1, jest taka sama jak pole powierzchni jednej kuli o promieniu
A) 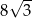 B) 8 C)
B) 8 C) 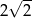 D) 2
D) 2
Liczba pięciocyfrowa  jest podzielna przez 3, ale nie jest podzielna przez 6. Trzy początkowe cyfry tej liczby to: 4, 1, 3, a dwie pozostałe cyfry są większe od 4. Ile może być równe
jest podzielna przez 3, ale nie jest podzielna przez 6. Trzy początkowe cyfry tej liczby to: 4, 1, 3, a dwie pozostałe cyfry są większe od 4. Ile może być równe  ? Podaj wszystkie możliwości. Odpowiedź uzasadnij.
? Podaj wszystkie możliwości. Odpowiedź uzasadnij.
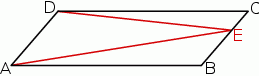
Na rysunku przedstawiono równoległobok 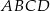 i trójkąt
i trójkąt 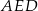 . Punkt
. Punkt 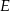 leży na odcinku
leży na odcinku 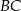 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 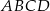 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta  .
.
Trzej bracia: Antek, Wojtek i Karol otrzymali po 12 zł kieszonkowego i postanowili kupić za te pieniądze dwa rodzaje słodyczy: lizaki i batony. Antek za swoje 12 zł kupił 3 lizaki i 6 batonów, a Wojtek za tę samą kwotę kupił 9 lizaków i 2 batony. Karol chciałby kupić 6 lizaków, a za resztę pieniędzy batony. Ile batonów może kupić Karol? Uzasadnij odpowiedź.

